비선형 시계열 알고리즘¶
상태 공간 모형(State Space Models)¶
“시계열 생성 구조를 관측식(Observation Equation)과 상태 전이식(State Transition Equation) 두 개의 수식으로 정의하는 시계열 모형”
관측식(Observation Equation)
: 현재의 상태 \(x_t\)와 잡음(에러) \(\upsilon_t\)에 의해 실제로 측정가능한 출력 \(y_t\)를 생성하는 관계식
\begin{align*}
y_t = f(x_t, \upsilon_t)
\end{align*}
상태 전이식(State Transition Equation)
: 이전의 상태 \(x_{t-1}\)와 현재 생성된 잡음(에러) \(w_t\)에 의해 현재의 상태 \(x_t\)가 생성되는 관계식
\begin{align*}
x_t = g(x_{t-1}, w_t)
\end{align*}
동적 시스템(Dynamic System)
: 입력 시계열을 받아 출력 시계열을 내놓는 시스템
: (예시) ARMA 모형의 경우 백색잡음 \(\epsilon_t\)를 입력받아 \(y_t\)를 출력하는 동적 시스템
상태 변수(State Variable)
: 동적 시스템의 현재 상태를 정의하는 값의 집합
: (예시) AR(\(p\)) 모형의 동적시스템은 \(p\)개의 과거 \(Y\)값 \(\{Y_{t-1}, Y_{t-2}, \cdots, Y_{t-p}\}\)이 상태변수
: (예시) ARMA(\(p,q\)) 모형의 동적시스템은 \(p\)개의 과거 \(Y\)값 \(\{Y_{t-1}, Y_{t-2}, \cdots, Y_{t-p}\}\)과 \(q\)개의 과거 \(\epsilon\)값 \(\{\epsilon_{t-1}, \epsilon_{t-2}, \cdots, \epsilon_{t-q}\}\)이 상태변수
\begin{align*} \text{Equation of AR}(p) && Y_t = \phi_1 Y_{t-1} + \cdots + \phi_p Y_{t-p} + \epsilon_t \end{align*}
\begin{align*} \text{Equation of ARMA}(p,q) && Y_t = \phi_1 Y_{t-1} + \cdots + \phi_p Y_{t-p} + \theta_1 \epsilon_{t-1} \cdots + \theta_q \epsilon_{t-q} + \epsilon_t \end{align*}
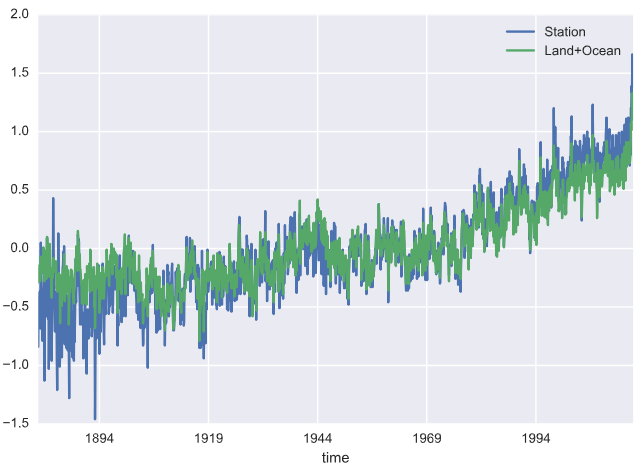
지수평활법(Simple Exponential Smoothing)¶
“추세나 계절성 패턴이 없는 경우 적합”
“미래 시계열 데이터는 과거 특정기간 동안의 평균값이며 그 이전의 값들은 미래에 어떠한 정보도 주지 않는다”
\begin{align*} \hat{Y}{t+1} & = \dfrac{1}{T}\displaystyle \sum{i=0}^{T} Y_{t-i} \ & or \ \hat{Y}{t+1} & = \dfrac{\alpha}{T}\displaystyle \sum{i=1}^{T} (1-\alpha)^i Y_{t-i} \ \end{align*}
import pandas as pd
from statsmodels.tsa.api import SimpleExpSmoothing
import matplotlib.pyplot as plt
location = './Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv'
raw_all = pd.read_csv(location)
# Simple Exponential Smoothing
target = raw_all.loc[:24*7*2, 'count']
target.plot(marker='o', color='black', legend=True, figsize=(20,6), ylim=(0,400))
fit1 = SimpleExpSmoothing(target).fit(smoothing_level=0.2, optimized=False)
fcast1 = fit1.forecast(24).rename(r'$\alpha=0.2$')
fcast1.plot(marker='o', color='blue', legend=True)
fit1.fittedvalues.plot(marker='o', color='blue')
fit2 = SimpleExpSmoothing(target).fit(smoothing_level=0.6, optimized=False)
fcast2 = fit2.forecast(24).rename(r'$\alpha=0.6$')
fcast2.plot(marker='o', color='red', legend=True)
fit2.fittedvalues.plot(marker='o', color='red')
fit3 = SimpleExpSmoothing(target).fit()
fcast3 = fit3.forecast(24).rename(r'$\alpha=%s$'%fit3.model.params['smoothing_level'])
fcast3.plot(marker='o', color='green', legend=True)
fit3.fittedvalues.plot(marker='o', color='green')
plt.show()
---------------------------------------------------------------------------
FileNotFoundError Traceback (most recent call last)
<ipython-input-1-b67374db9c10> in <module>
4
5 location = './Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv'
----> 6 raw_all = pd.read_csv(location)
7
8 # Simple Exponential Smoothing
~/opt/anaconda3/lib/python3.7/site-packages/pandas/io/parsers.py in parser_f(filepath_or_buffer, sep, delimiter, header, names, index_col, usecols, squeeze, prefix, mangle_dupe_cols, dtype, engine, converters, true_values, false_values, skipinitialspace, skiprows, skipfooter, nrows, na_values, keep_default_na, na_filter, verbose, skip_blank_lines, parse_dates, infer_datetime_format, keep_date_col, date_parser, dayfirst, cache_dates, iterator, chunksize, compression, thousands, decimal, lineterminator, quotechar, quoting, doublequote, escapechar, comment, encoding, dialect, error_bad_lines, warn_bad_lines, delim_whitespace, low_memory, memory_map, float_precision)
674 )
675
--> 676 return _read(filepath_or_buffer, kwds)
677
678 parser_f.__name__ = name
~/opt/anaconda3/lib/python3.7/site-packages/pandas/io/parsers.py in _read(filepath_or_buffer, kwds)
446
447 # Create the parser.
--> 448 parser = TextFileReader(fp_or_buf, **kwds)
449
450 if chunksize or iterator:
~/opt/anaconda3/lib/python3.7/site-packages/pandas/io/parsers.py in __init__(self, f, engine, **kwds)
878 self.options["has_index_names"] = kwds["has_index_names"]
879
--> 880 self._make_engine(self.engine)
881
882 def close(self):
~/opt/anaconda3/lib/python3.7/site-packages/pandas/io/parsers.py in _make_engine(self, engine)
1112 def _make_engine(self, engine="c"):
1113 if engine == "c":
-> 1114 self._engine = CParserWrapper(self.f, **self.options)
1115 else:
1116 if engine == "python":
~/opt/anaconda3/lib/python3.7/site-packages/pandas/io/parsers.py in __init__(self, src, **kwds)
1889 kwds["usecols"] = self.usecols
1890
-> 1891 self._reader = parsers.TextReader(src, **kwds)
1892 self.unnamed_cols = self._reader.unnamed_cols
1893
pandas/_libs/parsers.pyx in pandas._libs.parsers.TextReader.__cinit__()
pandas/_libs/parsers.pyx in pandas._libs.parsers.TextReader._setup_parser_source()
FileNotFoundError: [Errno 2] File ./Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv does not exist: './Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv'
선형 추세 알고리즘 by Holt¶
“간단 지수평활법에 추세를 반영한 예측 알고리즘”
\begin{align*}
\text{Main equation} && \hat{Y}{t+h} &= \ell{t} + hb_{t} \
\text{Level equation} && \ell_{t} &= \alpha Y_{t} + (1 - \alpha)(\ell_{t-1} + b_{t-1}) \
\text{Trend equation} && b_{t} &= \beta^(\ell_{t} - \ell_{t-1}) + (1 -\beta^)b_{t-1}
\end{align*}
\begin{align*} where~0 \leq \beta^* \leq 1~is~the~smoothing~parameter~for~the~trend \end{align*}
Year |
\(t\) |
\(Y_t\) |
\(ℓ_t\) |
\(b_t\) |
\(\hat{Y_t}\) |
|---|---|---|---|---|---|
2014 |
0 |
17.55 |
4.31 |
||
2015 |
1 |
17.55 |
18.41 |
3.62 |
21.86 |
2016 |
2 |
21.86 |
21.89 |
3.59 |
22.03 |
2017 |
3 |
23.89 |
24.21 |
3.33 |
25.48 |
2018 |
4 |
26.93 |
27.05 |
3.24 |
27.54 |
import warnings
warnings.filterwarnings('always')
warnings.filterwarnings('ignore')
import pandas as pd
from statsmodels.tsa.api import Holt
import matplotlib.pyplot as plt
location = './Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv'
raw_all = pd.read_csv(location)
# Holt's Linear Trend
target = raw_all.loc[:24*7*2, 'count']
target.plot(marker='o', color='black', legend=True, figsize=(20,6), ylim=(0,400))
fit1 = Holt(target).fit()
fcast1 = fit1.forecast(24).rename("Holt's linear trend")
fcast1.plot(marker='o', color='blue', legend=True)
fit1.fittedvalues.plot(marker='o', color='blue')
fit2 = Holt(target, exponential=True).fit()
fcast2 = fit2.forecast(24).rename("Exponential weighted trend")
fcast2.plot(marker='o', color='red', legend=True)
fit2.fittedvalues.plot(marker='o', color='red')
fit3 = Holt(target, damped=True).fit()
fcast3 = fit3.forecast(24).rename("Additive damped trend")
fcast3.plot(marker='o', color='green', legend=True)
fit3.fittedvalues.plot(marker='o', color='green')
plt.show()
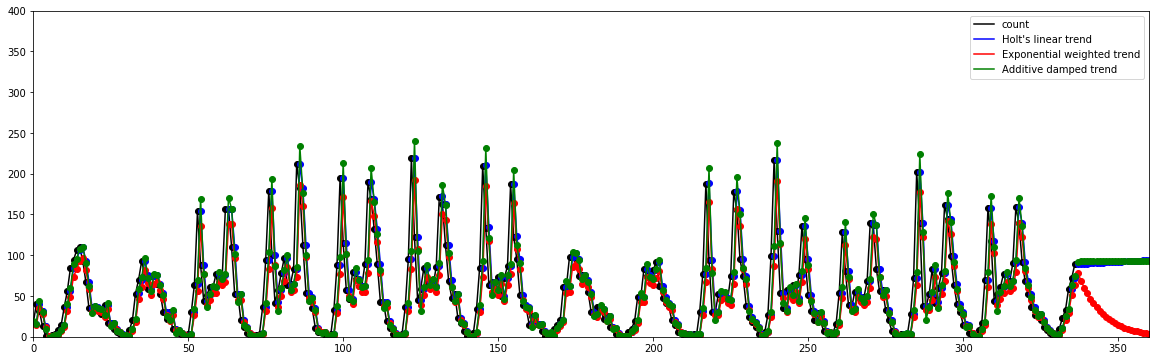
계절 알고리즘 by Holt-Winter¶
“선형 추세 알고리즘에 계절성을 반영한 예측 알고리즘”
Additive Seasonal Method: \(Y_t = T_t + S_t + R_t\), 계절성 변화의 크기가 시간 흐름에 따라 일정한 경우 선호
\begin{align*} \text{Main equation} && \hat{Y}{t+h} &= \ell{t} + hb_{t} + s_{t-m+h_{m}^{+}} \ \text{Level equation} && \ell_{t} &= \alpha(Y_{t} - s_{t-m}) + (1 - \alpha)(\ell_{t-1} + b_{t-1}) \ \text{Trend equation} && b_{t} &= \beta^(\ell_{t} - \ell_{t-1}) + (1 - \beta^)b_{t-1} \ \text{Seasonal equation} && s_{t} &= \gamma (y_{t}-\ell_{t-1}-b_{t-1}) + (1-\gamma)s_{t-m} \ \end{align*}
\begin{align*} where~h_{m}^{+} = \lfloor(h-1)/m\rfloor+1~ensures~that~estimates~of~the~sesonal~indices~come~from~the~final~year~of~the~sample \ \end{align*}
Multiplicative Seasonal Method: \(Y_t = T_t \times S_t \times R_t\), 계절성 변화의 크기가 시간 흐름에 비례하여 변경되는 경우 선호
\begin{align*} \text{Main equation} && \hat{Y}{t+h} &= (\ell{t} + hb_{t})s_{t-m+h_{m}^{+}} \ \text{Level equation} && \ell_{t} &= \alpha \frac{Y_{t}}{s_{t-m}} + (1 - \alpha)(\ell_{t-1} + b_{t-1}) \ \text{Trend equation} && b_{t} &= \beta^(\ell_{t}-\ell_{t-1}) + (1 - \beta^)b_{t-1} \ \text{Seasonal equation} && s_{t} &= \gamma \frac{y_{t}}{(\ell_{t-1} + b_{t-1})} + (1 - \gamma)s_{t-m} \ \end{align*}
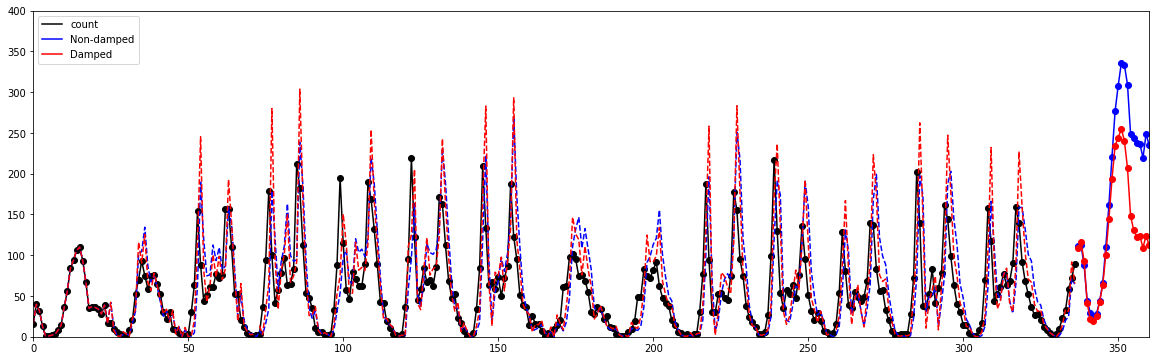
Damped Seasonal Method: Additive와 Multiplicative 모두 사용되며 장기 예측시 무한정 증가/감소를 방지
\begin{align*} \text{Main equation} && \hat{Y}{t+h} &= \left[\ell{t} + (\phi+\phi^2 + \dots + \phi^{h})b_{t}\right]s_{t+h-m(k+1)} \ \text{Level equation} && \ell_{t} &= \alpha(y_{t} / s_{t-m}) + (1 - \alpha)(\ell_{t-1} + \phi b_{t-1}) \ \text{Trend equation} && b_{t} &= \beta^(\ell_{t} - \ell_{t-1}) + (1 - \beta^)\phi b_{t-1} \ \text{Seasonal equation} && s_{t} &= \gamma \frac{y_{t}}{(\ell_{t-1} + \phi b_{t-1})} + (1 - \gamma)s_{t-m} \ \end{align*}
Summary of Smoothing Parameters:
Level |
Trend |
Seasonality |
Damping |
|---|---|---|---|
\(\alpha\) |
\(\beta\) |
\(\gamma\) |
\(\phi\) |
Example of Estimation Process:
- |
\(t\) |
\(Y_t\) |
\(\ell_t\) |
\(b_t\) |
\(s_t\) |
\(\hat{Y}_t\) |
|---|---|---|---|---|---|---|
2004 Q1 |
-3 |
- |
- |
- |
1.24 |
- |
2004 Q2 |
-2 |
- |
- |
- |
0.77 |
- |
2004 Q3 |
-1 |
- |
- |
- |
0.96 |
- |
2004 Q4 |
0 |
- |
32.49 |
0.7 |
1.02 |
- |
2005 Q1 |
1 |
42.21 |
33.51 |
0.71 |
1.24 |
41.29 |
2005 Q2 |
2 |
24.65 |
33.24 |
0.68 |
0.77 |
26.36 |
2005 Q3 |
3 |
32.67 |
33.94 |
0.68 |
0.96 |
32.62 |
2005 Q4 |
4 |
37.26 |
35.4 |
0.7 |
1.02 |
35.44 |
- |
⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
2015 Q1 |
41 |
73.26 |
58.57 |
0.66 |
1.24 |
72.59 |
2015 Q2 |
42 |
47.7 |
60.42 |
0.69 |
0.77 |
45.62 |
2015 Q3 |
43 |
61.1 |
62.17 |
0.72 |
0.96 |
58.77 |
2015 Q4 |
44 |
66.06 |
63.62 |
0.75 |
1.02 |
64.38 |
- |
\(h\) |
- |
- |
- |
- |
\(\hat{Y}_{T+h}\) |
2016 Q1 |
1 |
- |
- |
- |
- |
80.09 |
2016 Q2 |
2 |
- |
- |
- |
- |
50.15 |
2016 Q3 |
3 |
- |
- |
- |
- |
63.34 |
2016 Q4 |
4 |
- |
- |
- |
- |
68.18 |
2017 Q1 |
5 |
- |
- |
- |
- |
83.8 |
2017 Q2 |
6 |
- |
- |
- |
- |
52.45 |
2017 Q3 |
7 |
- |
- |
- |
- |
66.21 |
2017 Q4 |
8 |
- |
- |
- |
- |
71.23 |
import pandas as pd
from statsmodels.tsa.api import ExponentialSmoothing
import matplotlib.pyplot as plt
location = './Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv'
raw_all = pd.read_csv(location)
# Holt-Winter's Seasonal
target = raw_all.loc[:24*7*2, 'count']
target.plot(marker='o', color='black', legend=True, figsize=(20,6), ylim=(0,400))
fit1 = ExponentialSmoothing(target, seasonal_periods=24, trend='add', seasonal='add').fit(use_boxcox=True)
fcast1 = fit1.forecast(24).rename("Non-damped")
fcast1.plot(marker='o', color='blue', legend=True)
fit1.fittedvalues.plot(style='--', color='blue')
fit2 = ExponentialSmoothing(target, seasonal_periods=24, trend='add', seasonal='add', damped=True).fit(use_boxcox=True)
fcast2 = fit2.forecast(24).rename("Damped")
fcast2.plot(marker='o', color='red', legend=True)
fit2.fittedvalues.plot(style='--', color='red')
plt.show()
지수평활법 알고리즘 분류 요약¶
알고리즘 옵션 분류
Trend Component |
Seasonal Component |
- |
- |
|---|---|---|---|
- |
N |
A |
M |
- |
(None) |
(Additive) |
(Multiplicative) |
N (None) |
(N,N) |
(N,A) |
(N,M) |
A (Additive) |
(A,N) |
(A,A) |
(A,M) |
\(A_d\) (Additive damped) |
(\(A_d\),N) |
(\(A_d\),A) |
(\(A_d\),M) |
각 분류별 알고리즘
Short hand |
Method |
|---|---|
(N,N) |
Simple exponential smoothing |
(A,N) |
Holt’s linear method |
(\(A_d\),N) |
Additive damped trend method |
(A,A) |
Additive Holt-Winters’ method |
(A,M) |
Multiplicative Holt-Winters’ method |
(\(A_d\),M) |
Holt-Winters’ damped method |

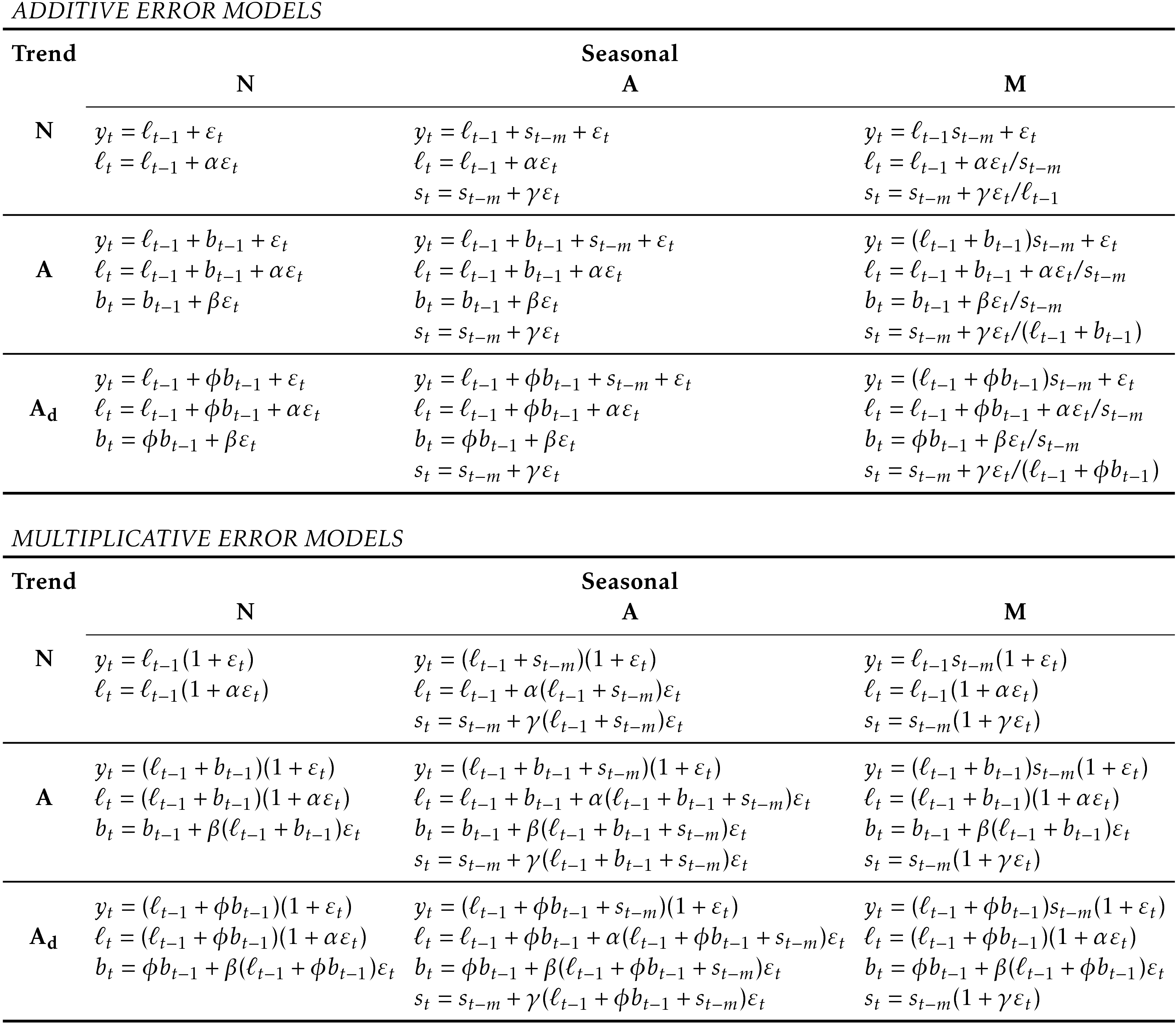
ETS(Error/Trend/Seasonal) 알고리즘¶
1) ETS(A,N,N): simple exponential smoothing with additive errors
2) ETS(M,N,N): simple exponential smoothing with multiplicative errors
3) ETS(A,A,N): Holt’s linear method with additive errors
4) ETS(M,A,N): Holt’s linear method with multiplicative errors
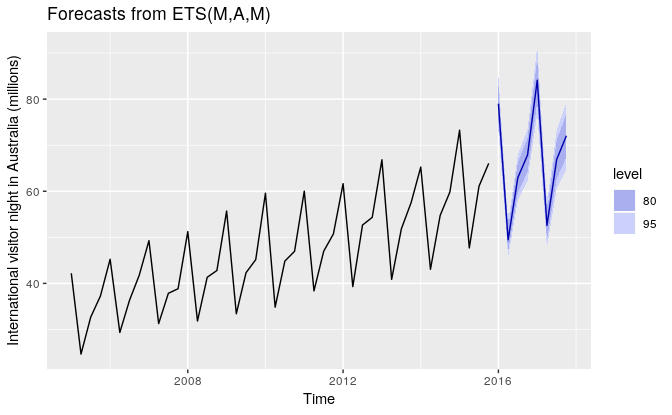
Model |
Forecast variance: \(\sigma_h^2\) |
|---|---|
(A,N,N) |
\(\sigma_h^2 = \sigma^2\big[1 + \alpha^2(h-1)\big]\) |
(A,A,N) |
\(\sigma_h^2 = \sigma^2\Big[1 + (h-1)\big\{\alpha^2 + \alpha\beta h + \frac16\beta^2h(2h-1)\big\}\Big]\) |
(A,\(A_d\),N) |
\(\sigma_h^2 = \sigma^2\biggl[1 + \alpha^2(h-1) + \frac{\beta\phi h}{(1-\phi)^2} \left\{2\alpha(1-\phi) +\beta\phi\right\} \\ \mbox{} - \frac{\beta\phi(1-\phi^h)}{(1-\phi)^2(1-\phi^2)} \left\{ 2\alpha(1-\phi^2)+ \beta\phi(1+2\phi-\phi^h)\right\}\biggr]\) |
(A,N,A) |
\(\sigma_h^2 = \sigma^2\Big[1 + \alpha^2(h-1) + \gamma k(2\alpha+\gamma)\Big]\) |
(A,A,A) |
\(\sigma_h^2 = \sigma^2\Big[1 + (h-1)\big\{\alpha^2 + \alpha\beta h + \frac16\beta^2h(2h-1)\big\} \\ \mbox{} + \gamma k \big\{2\alpha+ \gamma + \beta m (k+1)\big\} \Big]\) |
(A,\(A_d\),A) |
\(\sigma_h^2 = \sigma^2\biggl[1 + \alpha^2(h-1) + \gamma k(2\alpha+\gamma) \\ \mbox{} +\frac{\beta\phi h}{(1-\phi)^2} \left\{2\alpha(1-\phi) + \beta\phi \right\} \\ \mbox{} - \frac{\beta\phi(1-\phi^h)}{(1-\phi)^2(1-\phi^2)} \left\{ 2\alpha(1-\phi^2)+ \beta\phi(1+2\phi-\phi^h)\right\} \\ \mbox{} + \frac{2\beta\gamma\phi}{(1-\phi)(1-\phi^m)}\left\{k(1-\phi^m) - \phi^m(1-\phi^{mk})\right\}\biggr]\) |
상태공간 모형과 ARIMA 모형의 관계¶
동적 선형모형(Dynamics Linear Model) vs. ARIMA 모형
모든 ARIMA 모형은 동일한 출력(Measurement)을 가지는 동적 선형 모형으로 표현가능하며, 조합 방법은 무한함
모든 동적 선형모형 출력은 ARIMA 모형으로 표현 가능
상태공간모형 \(\Longrightarrow\) ARMA
\begin{align*} \text{Main Equation of State Space Model} && Y_{t} &= A_t X_{t} = A_t (I- \Phi_t L)^{-1} w_t \ \text{where} && X_{t} &= \Phi_t X_{t-1} + w_t \ && &= \Phi_t L X_{t} + w_t \ && (I- \Phi_t L) X_{t} &= w_t \ && X_{t} &= (I- \Phi_t L)^{-1} w_t \ \end{align*}
ARMA(p,q) \(\Longrightarrow\) 상태공간모형 : 상태변수를 정하는 방법이 무한하기에 표준형식(Canonical Form)을 따름
\begin{align*} \text{Main Equation of ARMA(p,q)} && Y_t &= \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \cdots + \phi_p Y_{t-p} + e_t + \theta_1 e_{t-1} + \theta_2 e_{t-2} + \cdots + \theta_q e_{t-q} \ \text{let \(r=max(p,q+1)\)} && Y_{t} &= \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \cdots + \phi_r Y_{t-r} + e_t + \theta_1 e_{t-1} + \theta_2 e_{t-2} + \cdots + \theta_{r-1} e_{t-(r-1)} \ \text{Insert State Space} && Y_t &= \begin{bmatrix} 1 & 0 & \cdots & 0 \end{bmatrix} \begin{bmatrix} x_{t,1} \ x_{t,2} \ \vdots \ x_{t,r-1} \ x_{t,r} \ \end{bmatrix} \ \text{where} && x_{1,t} &= \phi_1 x_{1,t-1} + x_{2,t-1} + e_t \ && x_{2,t} &= \phi_2 x_{1,t-1} + x_{3,t-1} + \theta_1 e_t \ && x_{3,t} &= \phi_3 x_{1,t-1} + x_{4,t-1} + \theta_2 e_t \ && & \vdots \ && x_{r-1,t} &= \phi_{r-1} x_{1,t-1} + x_{r,t-1} + \theta_{r-2} e_t \ && x_{r,t} &= \phi_{r} x_{1,t-1} + \theta_{r-1} e_t \ \text{Induced} && x_{1,t} &= \phi_1 x_{1,t-1} + \phi_2 x_{1,t-2} + \cdots + \phi_r x_{1,t-r} + e_t + \theta_1 e_t + \cdots + \theta_{r-1} e_{t-(r-1)} \ \text{State Space Form} && Y_t &= \begin{bmatrix} 1 & 0 & \cdots & 0 \end{bmatrix} \begin{bmatrix} x_{t,1} \ x_{t,2} \ \vdots \ x_{t,r-1} \ x_{t,r} \ \end{bmatrix} \ \text{where} && \begin{bmatrix} x_{t,1} \ x_{t,2} \ \vdots \ x_{t,r-1} \ x_{t,r} \ \end{bmatrix} &= \begin{bmatrix} \phi_1 & 1 & 0 & \cdots & 0 \ \phi_2 & 0 & 1 & \cdots & 0 \ \vdots & \vdots & \vdots & \ddots & \vdots \ \phi_{r-1} & 0 & 1 & \cdots & 1 \ \phi_r & 0 & 0 & \cdots & 0 \ \end{bmatrix} \begin{bmatrix} x_{t-1,1} \ x_{t-1,2} \ \vdots \ x_{t-1,r-1} \ x_{t-1,r} \ \end{bmatrix} + \begin{bmatrix} 1 & \theta_1 & \cdots & \theta_{r-1} \end{bmatrix} \begin{bmatrix} e_{1} \ e_{2} \ \vdots \ e_{r-1} \ e_{r} \ \end{bmatrix} \end{align*}
ARIMA(p,d,q) \(\Longrightarrow\) 상태공간모형 : \(\Delta^d Y_t = ARMA(p,q)\)
\begin{align*} \text{Each Equation of \(\Delta^d Y_t\)} && \Delta^{1} Y_{t} &= Y_t - Y_{t-1} \ && \Delta^{2} Y_{t} &= \Delta^{1} Y_{t}- \Delta^{1} Y_{t-1} \ && & \vdots \ && \Delta^{d} Y_{t} &= \Delta^{d-1} Y_{t}- \Delta^{d-1} Y_{t-1} \ \text{State Space Form} && Y_t &= \begin{bmatrix} 1 & 1 & \cdots & 1 & 1 & 0 & \cdots & 0 \end{bmatrix} \begin{bmatrix} Y_{t} \ \Delta Y_{t-1} \ \vdots \ \Delta^{d-1} Y_{t-1} \ \Delta^{d} Y_{t-1} \ x_{t,2} \ \vdots \ x_{t,r-1} \ x_{t,r} \ \end{bmatrix} \ \text{where} && \begin{bmatrix} Y_{t-1} \ \Delta Y_{t-1} \ \vdots \ \Delta^{d-1} Y_{t-1} \ \Delta^{d} Y_{t} \ x_{t,2} \ \vdots \ x_{t,r-1} \ x_{t,r} \ \end{bmatrix} &= \begin{bmatrix} 1 & 1 & \cdots & 1 & 1 & 0 & 0 &\cdots & 0 \ 0 & 1 & \cdots & 1 & 1 & 0 & 0 &\cdots & 0 \ \vdots & \vdots & \vdots & \vdots & \vdots & 0 & 0 &\cdots & 0 \ 0 & 0 & \cdots & 1 & 1 & 0 & 0 & \cdots & 0 \ 0 & 0 & \cdots & 0 & \phi_1 & 1 & 0 & \cdots & 0 \ 0 & 0 & \cdots & 0 & \phi_2 & 0 & 1 & \cdots & 0 \ 0 & 0 & \cdots & 0 & \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 & \phi_{r-1} & 0 & 1 & \cdots & 1 \ 0 & 0 & \cdots & 0 & \phi_r & 0 & 0 & \cdots & 0 \ \end{bmatrix} \begin{bmatrix} Y_{t-2} \ \Delta Y_{t-2} \ \vdots \ \Delta^{d-1} Y_{t-2} \ \Delta^{d} Y_{t-1} \ x_{t-1,2} \ \vdots \ x_{t-1,r-1} \ x_{t-1,r} \ \end{bmatrix} \ && &+ \begin{bmatrix} 0 & \cdots & 0 & 1 & \theta_1 & \cdots & \theta_{r-1} \end{bmatrix} \begin{bmatrix} 0 \ 0 \ \vdots \ 0 \ e_{1} \ e_{2} \ \vdots \ e_{r-1} \ e_{r} \ \end{bmatrix} \end{align*}
로컬레벨 모형(Local Level Model)¶
랜덤워크 모형에 관측잡음이 추가된 것으로 랜덤워크 과정을 따르는 단변수 상태변수 \(\mu_t\)를 가짐 \begin{align*} \mu_t &= \mu_{t-1} + w_t &,;;; & w_t \sim N(0, \sigma_w^2) \ Y_{t} &= \mu_{t} + v_t &,;;; & v_t \sim {N}(0, \sigma_v^2) \ \end{align*}
로컬레벨 모형 \(\Longrightarrow\) ARIMA 모형
로컬레벨 모형은 ARIMA(0,1,1)의 다른표현
\(\Delta Y_t\)는 \(MA(1)\) 모형을 따르고 \(Y_t\)는 \(ARIMA(0,1,1)\) 모형을 따름
\begin{align*} \text{Setting of \(\mu_t\)} && \mu_t &= Y_t - v_t \ \text{Equation of Local Level Model} && Y_t - v_t &= Y_{t-1} - v_{t-1} + w_t \ \text{Equation of ARIMA Model} && \Delta Y_t &= Y_t - Y_{t-1} = w_t + v_t - v_{t-1} \ \text{Expectation} && \text{E} \left( \Delta Y_t \right) &= \text{E} \left( w_t + v_t - v_{t-1} \right) =0 \ \text{Variance} && \text{E} ( \Delta Y_t^2 ) &= \text{E} \left[ (w_t + v_t - v_{t-1})(w_{t} + v_{t} - v_{t-1}) \right] \ && &= \text{E} \left( w_t^2 + v_t^2 + v_{t-1}^2 \right) \ && &= \sigma_w^2 + 2\sigma_v^2 \ \text{Autocorrelation(1)} && \text{E} ( \Delta Y_t \Delta Y_{t-1} ) &= \text{E} \left[ (w_t + v_t - v_{t-1})(w_{t-1} + v_{t-1} - v_{t-2}) \right] \ && &= - \text{E} \left( v_{t-1}^2 \right) \ && &= -\sigma_v^2 \ \text{Autocorrelation(\(l\))} && \text{E} ( \Delta Y_t \Delta Y_{t-l} ) &= 0, ;;; \text{for } l > 1 \end{align*}
ARIMA 모형과의 차이점:
ARIMA(0,1,1)이 아닌 로컬 레벨 모형을 사용하는 이유는 다음과 같이 이유와 가정 때문
우리가 관심을 가지는 값은 어떤 이유에 의해 반드시 랜덤 워크 모형을 따라야 한다.
그런데 시계열 자료 \(Y_t\)는 랜덤 워크 모형을 따르지 않는다. (ARIMA(0,1,1) 모형을 따름)
그러므로 시계열 자료 \(Y_t\)는 우리가 원하는 랜덤 워크 \(\mu_t\)에 관측 잡음이 더해진 걸로 가정하자.
이제 변경된 풀어야 하는 문제는 시계열 자료 \(Y_t\)를 사용하여 랜덤 워크 모형을 따르는, 잡음을 제거한 원래의 값 \(\mu_t\)이다.
예시문제1:
어떤 섬 근처에서 배가 엔진을 끄고 정지해 있다.
이 배는 파도에 의한 브라운 운동(Brown montion)을 하게 된다.
파도의 랜덤한 힘에 밀려 배의 위치는 다음과 같은 수식으로 변화된다.
\begin{align*} \mu_t = \mu_{t-1} + w_t \end{align*}매 시간마다 배의 선원은 섬으로부터의 거리 \(Y_t\)를 배에 있는 초음파 거리계(ultrasonic range finder)로 측정한다.
이러한 경우에 정확한 거리 \(\mu_t\)를 알고자 하는 것이 바로 로컬 레벨 모형의 필터링(filtering) 문제가 된다.
예시문제2:
효율적인 시장에서 거래되는 주식의 가격, 즉 주가는 일반적으로 랜덤 워크를 따르는 것으로 생각할 수 있다.
시장 미시구조 잡음이 있는 주가로부터 근본적인 주식의 내재 가치 즉, 랜덤 워크를 따르는 가치를 추정하고자 하는 경우도 로컬 레벨 모형의 필터링 문제로 볼 수 있다.
실습: 로컬레벨 모형 데이터생성 및 이해¶
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.statespace.kalman_filter import KalmanFilter
# 데이터 생성
np.random.seed(123)
model_generator = KalmanFilter(k_endog=1, k_states=1,
transition=[[1]], selection=[[1]], state_cov=[[1]],
design=[[1]], obs_cov=[[1]])
y_gener, x_gener = model_generator.simulate(100)
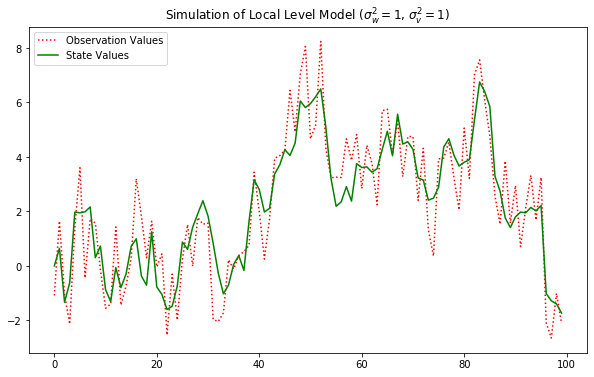
# 데이터 생성
plt.figure(figsize=(10,6))
plt.plot(y_gener, 'r:', label="Observation Values")
plt.plot(x_gener, 'g-', label="State Values")
plt.legend()
plt.title("Simulation of Local Level Model ($\sigma_w^2 = 1$, $\sigma_v^2 = 1$)")
plt.show()
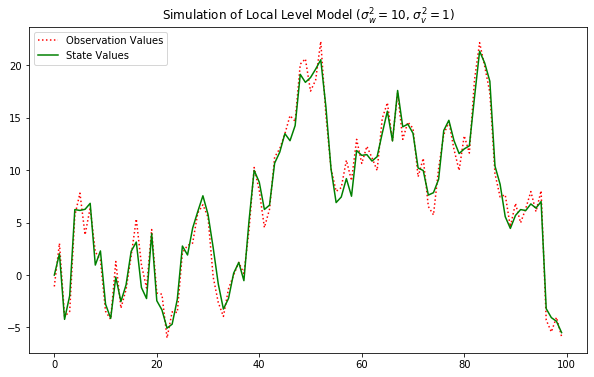
# 데이터 생성
np.random.seed(123)
model_generator = KalmanFilter(k_endog=1, k_states=1,
transition=[[1]], selection=[[1]], state_cov=[[10]],
design=[[1]], obs_cov=[[1]])
y_gener, x_gener = model_generator.simulate(100)
# 데이터 생성
plt.figure(figsize=(10,6))
plt.plot(y_gener, 'r:', label="Observation Values")
plt.plot(x_gener, 'g-', label="State Values")
plt.legend()
plt.title("Simulation of Local Level Model ($\sigma_w^2 = 10$, $\sigma_v^2 = 1$)")
plt.show()
# 데이터 생성
np.random.seed(123)
model_generator = KalmanFilter(k_endog=1, k_states=1,
transition=[[1]], selection=[[1]], state_cov=[[1]],
design=[[1]], obs_cov=[[10]])
y_gener_target, x_gener_target = model_generator.simulate(100)
# 데이터 생성
plt.figure(figsize=(10,6))
plt.plot(y_gener_target, 'r:', label="Observation Values")
plt.plot(x_gener_target, 'g-', label="State Values")
plt.legend()
plt.title("Simulation of Local Level Model ($\sigma_w^2 = 10$, $\sigma_v^2 = 1$)")
plt.show()
# 로컬레벨모형 추정
fit = sm.tsa.UnobservedComponents(y_gener_target, level='local level').fit()
fit.summary()
| Dep. Variable: | y | No. Observations: | 100 |
|---|---|---|---|
| Model: | local level | Log Likelihood | -279.818 |
| Date: | Fri, 13 Mar 2020 | AIC | 563.636 |
| Time: | 23:32:03 | BIC | 568.827 |
| Sample: | 0 | HQIC | 565.736 |
| - 100 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2.irregular | 13.0642 | 2.660 | 4.911 | 0.000 | 7.850 | 18.278 |
| sigma2.level | 0.7263 | 0.431 | 1.684 | 0.092 | -0.119 | 1.572 |
| Ljung-Box (Q): | 43.72 | Jarque-Bera (JB): | 1.48 |
|---|---|---|---|
| Prob(Q): | 0.32 | Prob(JB): | 0.48 |
| Heteroskedasticity (H): | 1.01 | Skew: | 0.06 |
| Prob(H) (two-sided): | 0.98 | Kurtosis: | 2.41 |
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
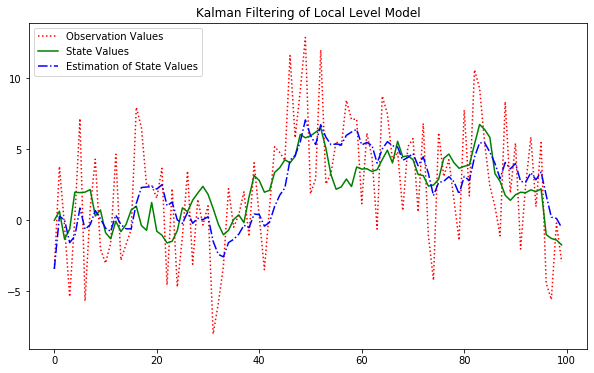
# 추정치 시각화
plt.figure(figsize=(10,6))
plt.plot(y_gener_target, 'r:', label="Observation Values")
plt.plot(x_gener_target, 'g-', label="State Values")
plt.plot(fit.filtered_state[0], 'b-.', label="Estimation of State Values")
plt.legend()
plt.title("Kalman Filtering of Local Level Model")
plt.show()
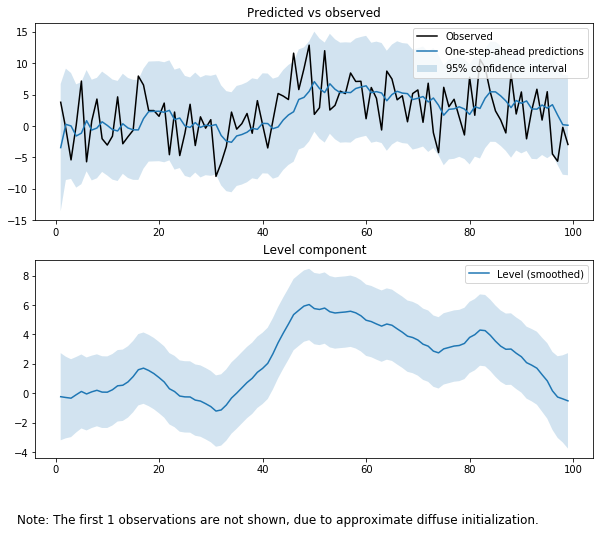
# 레벨추정 성분 시각화
fit.plot_components(figsize=(10,8))
plt.show()
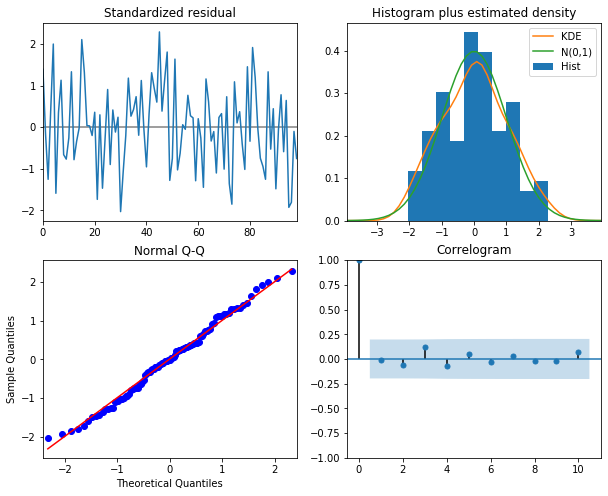
# 잔차진단
fit.plot_diagnostics(figsize=(10,8))
plt.show()
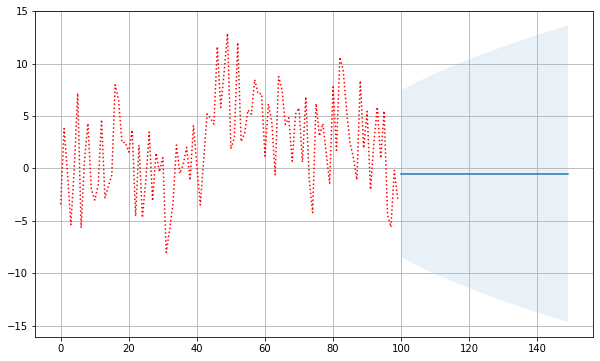
# 예측
plt.figure(figsize=(10,6))
forecast = fit.get_forecast(50)
plt.plot(y_gener_target, 'r:', label="Observation Values")
forecast_ci = forecast.conf_int()
forecast_index = np.arange(len(y_gener_target), len(y_gener_target) + len(forecast_ci))
plt.plot(forecast_index, forecast.predicted_mean, label="Observation Values")
plt.fill_between(forecast_index, forecast_ci[:, 0], forecast_ci[:, 1], alpha=0.1)
plt.grid()
plt.show()
로컬선형레벨 모형¶
랜덤 워크 모형의 관측값이 다시 누적된 것으로 랜덤워크 과정을 따르는 단변수 상태변수 \(\beta_t\)를 가짐 \begin{align*} && \beta_t &= \beta_{t-1} + w_{\beta,t} &,;;; & w_{\beta,t} \sim N(0, \sigma_\beta^2) \ && \mu_t &= \mu_{t-1} + \beta_{t-1} + w_{\mu,t} &,;;; & w_{\mu,t} \sim N(0, \sigma_\mu^2) \ && Y_{t} &= \mu_{t} + v_t &,;;; & v_t \sim {N}(0, \sigma_v^2) \ \text{Matrix Form} && \begin{bmatrix} \beta_t \ \mu_t \end{bmatrix} &= \begin{bmatrix} 1 & 0 \ 1 & 1 \ \end{bmatrix} \begin{bmatrix} \beta_{t-1} \ \mu_{t-1} \end{bmatrix}
\begin{bmatrix} w_{\beta,t} \ w_{\mu,t} \end{bmatrix} \end{align*}
로컬선형레벨 모형 \(\Longrightarrow\) ARIMA 모형
로컬선형레벨 모형은 ARIMA(0,2,2)의 다른표현
\(\Delta^2 Y_t\)는 \(MA(2)\) 모형을 따르고 \(Y_t\)는 \(ARIMA(0,2,2)\) 모형을 따름
\begin{align*} \text{Setting of \(\mu_t\)} && \mu_t &= Y_t - v_t \ \text{Equation of Local Level Model} && Y_t - v_t &= Y_{t-1} - v_{t-1} + \beta_{t-1} + w_{\mu,t} \ && \Delta Y_t &= Y_t - Y_{t-1} = \beta_{t-1} + w_{\mu,t} + v_t - v_{t-1} \ \text{Equation of Local Level Model(\(\beta\))} && \beta_{t-1} &= \Delta Y_t - w_{\mu,t} - v_t + v_{t-1} \ && \Delta Y_{t+1} - w_{\mu,t+1} - v_{t+1} + v_{t} &= \Delta Y_t - w_{\mu,t} - v_t + v_{t-1} + w_{\beta,t} \ && \Delta Y_{t+1} - \Delta Y_t &= w_{\mu,t+1} + v_{t+1} - v_{t} - w_{\mu,t} - v_t + v_{t-1} + w_{\beta,t} \ \text{Equation of ARIMA Model} && \Delta^2 Y_{t+1} &= w_{\mu,t+1} + v_{t+1} - v_{t} - w_{\mu,t} - v_t + v_{t-1} + w_{\beta,t} \ \end{align*}
예시문제1:
어떤 섬 근처에서 배가 엔진을 끄고 정지해 다가 어느 시점에 일정 속도로 움직이기 시작했다.
배의 속도 \(\beta_t\)는 일정하게 유지하고자 하지만 기관의 특성상 조금씩 속도의 변화가 누적될 수 있고, 이 속도 변화 \(w_{\beta,t}\)는 가우시안 정규 분포를 따른다고 가정하자.
또한 배의 속도 \(\beta_t\)에 의해 배의 위치 \(\mu_t\)는 변화하게 되는데 이 경우에도 파도의 힘에 의해 조금씩 앞뒤로 위치가 바뀔 수 있고 이 미세한 위치 변화 \(w_{\mu,t}\)도 가우시안 정규 분포를 따른다고 가정하자.
매 시간마다 배의 선원은 섬으로부터의 거리 \(Y_t\)를 배에 있는 초음파 거리계(ultrasonic range finder)로 측정한다.
이러한 경우에 정확한 거리 \(\mu_t\)를 알고자 하는 것이 바로 로컬 레벨 모형의 필터링(filtering) 문제가 된다.
(*로컬 선형 추세 모형은 오차가 큰 GPS 신호를 사용한 네비게이션에서 차량의 정확한 위치를 추정하는데도 사용된다.)
예시문제2:
거시경제(macro economics) 모형에서 사용하는 대부분의 지표값은 시간이 지나며 선형적 혹은 지수함수적으로 증가하는 경우가 많다.
이러한 시계열 값은 모두 로컬 선형 추세 모형으로 모형화가 가능하다.
실습: 로컬선형레벨 모형 데이터생성 및 이해¶
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.statespace.kalman_filter import KalmanFilter
# 데이터 생성
np.random.seed(0)
model_generator = KalmanFilter(k_endog=1, k_states=2, transition=[[1, 0], [1, 1]],
state_intercept=[[0], [3]], selection=[[1, 0], [0, 1]], state_cov=[[1, 0], [0, 1]],
design=[[0, 1]], obs_cov=[[500]])
y_gener, x_gener = model_generator.simulate(100)
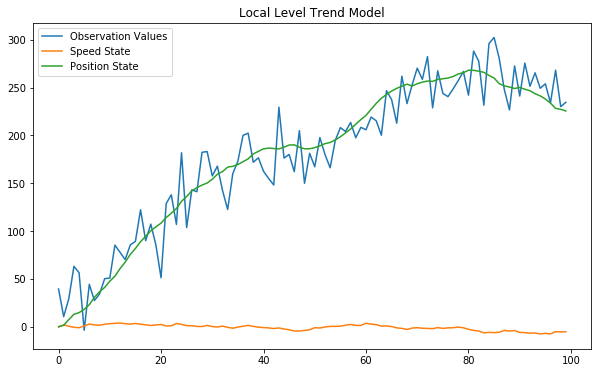
# 데이터 생성
plt.figure(figsize=(10,6))
plt.plot(y_gener, label="Observation Values")
plt.plot(x_gener.T[0], label="Speed State")
plt.plot(x_gener.T[1], label="Position State")
plt.legend()
plt.title("Local Level Trend Model")
plt.show()
# 로컬선형레벨모형 추정
fit = sm.tsa.UnobservedComponents(y_gener, level='local linear trend').fit()
fit.summary()
| Dep. Variable: | y | No. Observations: | 100 |
|---|---|---|---|
| Model: | local linear trend | Log Likelihood | -454.188 |
| Date: | Fri, 13 Mar 2020 | AIC | 914.377 |
| Time: | 23:32:12 | BIC | 922.132 |
| Sample: | 0 | HQIC | 917.513 |
| - 100 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2.irregular | 455.8288 | 79.801 | 5.712 | 0.000 | 299.423 | 612.235 |
| sigma2.level | 2.012e-06 | 28.472 | 7.07e-08 | 1.000 | -55.805 | 55.805 |
| sigma2.trend | 0.4817 | 0.497 | 0.969 | 0.332 | -0.492 | 1.456 |
| Ljung-Box (Q): | 48.05 | Jarque-Bera (JB): | 0.72 |
|---|---|---|---|
| Prob(Q): | 0.18 | Prob(JB): | 0.70 |
| Heteroskedasticity (H): | 0.68 | Skew: | -0.15 |
| Prob(H) (two-sided): | 0.28 | Kurtosis: | 2.72 |
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
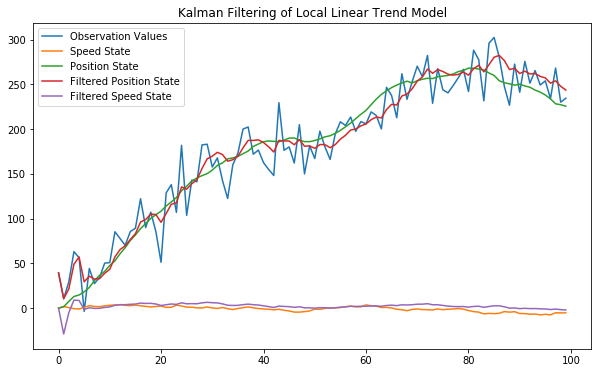
# 추정치 시각화
plt.figure(figsize=(10,6))
plt.plot(y_gener, label="Observation Values")
plt.plot(x_gener.T[0], label="Speed State")
plt.plot(x_gener.T[1], label="Position State")
plt.plot(fit.filtered_state[0], label="Filtered Position State")
plt.plot(fit.filtered_state[1], label="Filtered Speed State")
plt.legend()
plt.title("Kalman Filtering of Local Linear Trend Model")
plt.show()
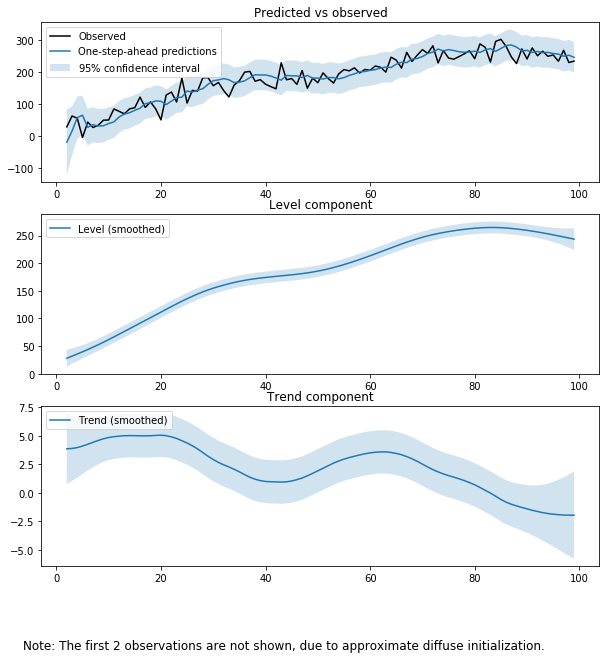
# 레벨추정 성분 시각화
fit.plot_components(legend_loc=2, figsize=(10,10))
plt.show()
# 잔차진단
fit.plot_diagnostics(figsize=(10,8))
plt.show()
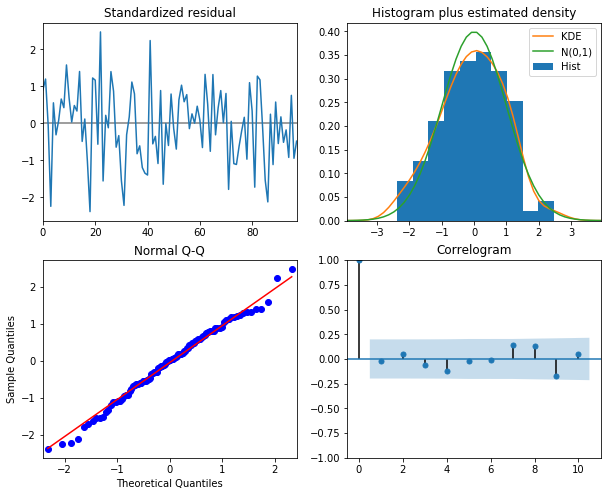
# 예측
plt.figure(figsize=(10,6))
forecast = fit.get_forecast(50)
plt.plot(y_gener, 'r:', label="Observation Values")
forecast_ci = forecast.conf_int()
forecast_index = np.arange(len(y_gener), len(y_gener) + len(forecast_ci))
plt.plot(forecast_index, forecast.predicted_mean, label="Observation Values")
plt.fill_between(forecast_index, forecast_ci[:, 0], forecast_ci[:, 1], alpha=0.1)
plt.grid()
plt.show()
상태공간모형 기반의 시계열 “구조화모형”¶
개별적 동적 특성(Dynamics, Transition Equation)을 정의할 수 있는 성분의 합 등으로 구성된 모형을 구조적 모형 또는 구조화 모형(Structural Model)
로컬 선형추세 모형에서 볼 수 있듯 상태공간모형의 장점은 실제로 관측된 하나의 시계열 자료로 부터 복수의 상태변수 시계열자료를 추정할 수 있다는 점
각각의 상태변수가 동적특성(Dynamics), 즉 상태 전이식(State Transition Equantion)에 대한 가정 필요
하나의 시계열 자료가 실제 여러개의 보이지 않는 성분들(Unobserved Components)이 합쳐진 것이라고 가정하고 각각의 성분을 추정하는 것이 가능(시계열 성분분리 가능)
각 성분의 동적특성을 이미 알거나 가정해야 하며 각 동적 특성이 구별가능할 정도로 충분이 달라야 함
보이지 않는 성분을 추정하는 모형이므로 Unobserved Component 모형이라고도 불림
예시: 시계열 = 추세성분 + 계절성성분 + ARMA성분
\begin{align*} \text{Main Equation} && Y_{T} &= T_{t} + S_{t} + A_{t} \ \text{Each Equations} && T_{t} &= \Phi_T T_{t-1} + w_{T,t} \ && S_{t} &= \Phi_S S_{t-1} + w_{S,t} \ && A_{t} &= \Phi_A A_{t-1} + w_{A,t} \ \text{Matrix Form} && Y_{T} &= \begin{bmatrix} 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} T_{t} \ S_{t} \ A_{t} \ \end{bmatrix}
v_t \ \text{where} && \begin{bmatrix} T_{t} \ S_{t} \ A_{t} \ \end{bmatrix} &= \begin{bmatrix} \Phi_T & 0 & \ 0 & \Phi_S & 0 \ 0 & 0 & \Phi_A \ \end{bmatrix} \begin{bmatrix} T_{t-1} \ S_{t-1} \ A_{t-1} \ \end{bmatrix}
\begin{bmatrix} w_{T,t} \ w_{S,t} \ w_{A,t} \ \end{bmatrix} \ \end{align*}
구조화모형 성분:
추세(Trend) 성분
계절성(Seasonal) 성분
주기적(Cyclical) 성분
AR(Autoregressive) 성분
회귀(Regression) 성분
1) 추세(Trend) 성분: 로컬레벨 모형이나 로컬선형추세 모형도 추세성분 모형의 일종
레벨모형 \begin{align*} \text{Fixed Intercept} && y_t &= \mu \ \text{Deterministic Constant} && y_t &= \mu + \varepsilon_t \ \text{Local Level} && y_t &= \mu_t + \varepsilon_t \ && \mu_t &= \mu_{t-1} + \eta_t \ \end{align*}
결정론적 추세 \begin{align*} \text{Fixed Slope} && y_t &= \mu_t \ && \mu_t &= \mu_{t-1} + \beta \ \text{Deterministic Trend} && y_t &= \mu_t + \varepsilon_t \ && \mu_t &= \mu_{t-1} + \beta \ \text{Local Linear Deterministic Trend} && y_t &= \mu_t + \varepsilon_t \ && \mu_t &= \mu_{t-1} + \beta + \eta_t \ \end{align*}
확률론적 추세 \begin{align*} \text{Random Walk} && y_t &= \mu_t \ && \mu_t &= \mu_{t-1} + \eta_t \ \text{Random Walk with Drift} && y_t &= \mu_t \ && \mu_t &= \mu_{t-1} + \beta + \eta_t \ \text{Local Linear Trend} && y_t &= \mu_t + \varepsilon_t \ && \mu_t &= \mu_{t-1} + \beta_{t-1} + \eta_t \ && \beta_t &= \beta_{t-1} + \zeta_t \ \end{align*}
2) 계절성(Seasonality) 성분: 주기가 명확한 성분
분기/월/요일/시간 등에 결정되는 반복적 요소는 계절성 성분, 주기적(Cyclical) 성분과는 구분됨
주기내의 값이 원래 일정(Level or Flat)해야 하는 것이 주기성에 의해 흔들린다고 보는 것
계절성 성분은 한 주기 내 각 성분의 합이 0이 되는 모형을 사용하며, 여기에 추가적으로 가우시안 잡음이 더해질 수 있음
예시: 4개의 계절성을 가지는 경우
\begin{align*} \text{4 Seasonality} && S_t + S_{t-1} + S_{t-2} + S_{t-3} &= w_{S,t} \ \text{Matrix Form} && \begin{bmatrix} S_{t} \ S_{t-1} \ S_{t-2} \ \end{bmatrix} &= \begin{bmatrix} -1 & -1 & -1 \ 1 & 0 & 0 \ 0 & 1 & 0 \ \end{bmatrix} \begin{bmatrix} S_{t-1} \ S_{t-2} \ S_{t-3} \ \end{bmatrix}
\begin{bmatrix} w_{S, t} \ 0 \ 0 \ \end{bmatrix} \ \end{align*}
3) 주기적(Cyclical) 성분: 주기가 명확하지 않거나 크기가 일정하지 않은 성분
모수 \(\lambda_c\)를 가지는 하모닉 상태 변수 쌍(pair)으로 모형화가 가능
만약 \(\rho_c\)가 1보다 작으면 점차 감소하는(damped) 주기적 성분
\begin{align*} \text{Pairwise Cycle} && c_{t} & = \rho_c ( \tilde c_{t} \cos \lambda_c t + \tilde c_{t}^* \sin \lambda_c t) + \tilde w_{t} \ && c_{t}^* & = \rho_c (- \tilde c_{t} \sin \lambda_c t + \tilde c_{t}^* \cos \lambda_c t) + \tilde w_{t}^* \ \text{Matrix Form} && \begin{bmatrix} c_{t} \ c_{t}^* \ \end{bmatrix} &= \rho_c \begin{bmatrix} \cos \lambda_c t & \sin \lambda_c t \ -\sin \lambda_c t & \cos \lambda_c t \ \end{bmatrix} \begin{bmatrix} c_{t-1} \ c_{t-1}^* \ \end{bmatrix}
\begin{bmatrix} w_{C, t} \ w_{C, t}^* \ \end{bmatrix} \ && & \text{(행렬식의 계수는 시간에 따라 계속 변화함)} \end{align}
4) AR 성분: 일반적인 AR(p) 성분 모형도 상태 변수 형태로 변환 가능
5) 회귀 성분: 내부 이노베이션 과정을 입력으로 가지는 것이 아니라 외부(Exogenous) 입력신호를 선형회귀식 형태로 가지는 성분
실습: 구조화모형을 사용한 성분 분리¶
\begin{align*} y_t & = \mu_t + \eta_t \ \mu_{t+1} & = \mu_t + \epsilon_{t+1} \ \eta_{t+1} & = \eta_t \cos \lambda_\eta + \eta_t^* \sin \lambda_\eta + \tilde \omega_t \qquad & \tilde \omega_t \sim N(0, \sigma_{\tilde \omega}^2) \ \eta_{t+1}^* & = -\eta_t \sin \lambda_\eta + \eta_t^* \cos \lambda_\eta + \tilde \omega_t^* & \tilde \omega_t^* \sim N(0, \sigma_{\tilde \omega}^2) \end{align*}
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.statespace.kalman_filter import KalmanFilter
import pandas_datareader.data as web
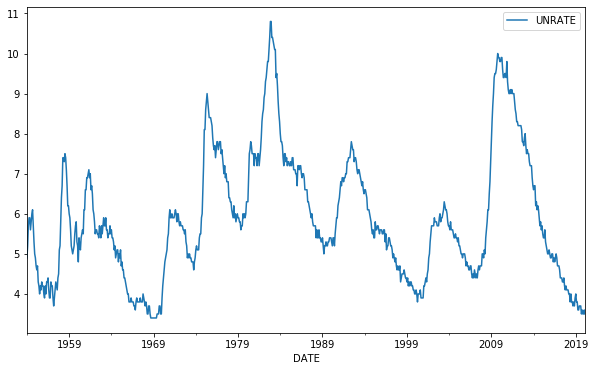
# 데이터 로딩
unemployment_US = web.DataReader('UNRATE', 'fred', start='1954-01-01')
unemployment_US.plot(figsize=(10,6))
plt.show()
# 구조화모형 추정
model = sm.tsa.UnobservedComponents(unemployment_US, level='rwalk', cycle=True,
stochastic_cycle=True, damped_cycle=True)
result = model.fit(method='powell')
display(result.summary())
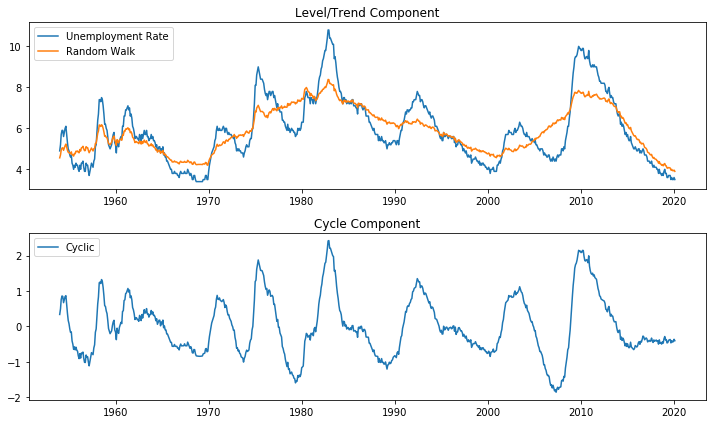
# 추정 시각화
fig, axes = plt.subplots(2, figsize=(10,6))
axes[0].plot(unemployment_US.index, unemployment_US.UNRATE, label='Unemployment Rate')
axes[0].plot(unemployment_US.index, result.level.smoothed, label='Random Walk')
axes[0].legend(loc='upper left')
axes[0].set(title='Level/Trend Component')
axes[1].set(title='Cycle Component')
axes[1].plot(unemployment_US.index, result.cycle.smoothed, label='Cyclic')
axes[1].legend(loc='upper left')
fig.tight_layout()
plt.show()
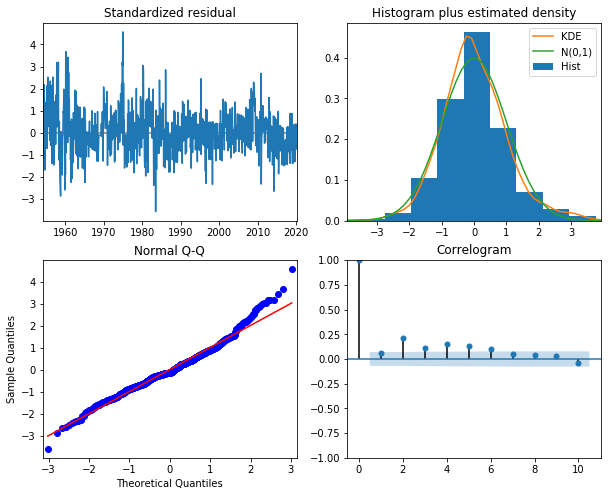
# 잔차진단
result.plot_diagnostics(figsize=(10,8))
plt.show()
Optimization terminated successfully.
Current function value: -0.278485
Iterations: 8
Function evaluations: 424
| Dep. Variable: | UNRATE | No. Observations: | 794 |
|---|---|---|---|
| Model: | random walk | Log Likelihood | 221.117 |
| + damped stochastic cycle | AIC | -434.235 | |
| Date: | Fri, 13 Mar 2020 | BIC | -415.541 |
| Time: | 23:32:22 | HQIC | -427.050 |
| Sample: | 01-01-1954 | ||
| - 02-01-2020 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2.level | 0.0146 | 0.005 | 2.879 | 0.004 | 0.005 | 0.025 |
| sigma2.cycle | 0.0167 | 0.005 | 3.403 | 0.001 | 0.007 | 0.026 |
| frequency.cycle | 0.0698 | 0.005 | 13.611 | 0.000 | 0.060 | 0.080 |
| damping.cycle | 0.9896 | 0.004 | 238.884 | 0.000 | 0.982 | 0.998 |
| Ljung-Box (Q): | 170.99 | Jarque-Bera (JB): | 86.95 |
|---|---|---|---|
| Prob(Q): | 0.00 | Prob(JB): | 0.00 |
| Heteroskedasticity (H): | 0.48 | Skew: | 0.48 |
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 4.32 |
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
주기적 성분 대신 AR(4) 모형 대체
\begin{align*} y_t & = \mu_t + \eta_t \ \mu_{t+1} & = \mu_t + \epsilon_{t+1} \ \phi(L) \eta_t & = \nu_t \end{align*}
# 구조화모형 추정
model = sm.tsa.UnobservedComponents(unemployment_US, level='rwalk', autoregressive=4)
result = model.fit(method='powell')
display(result.summary())
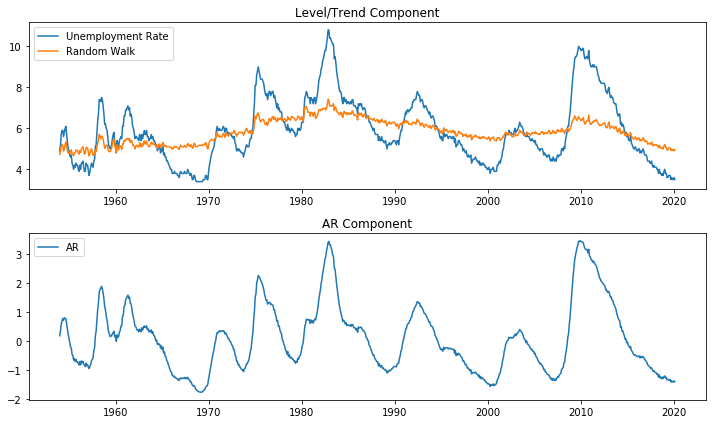
# 추정 시각화
fig, axes = plt.subplots(2, figsize=(10,6))
axes[0].plot(unemployment_US.index, unemployment_US.UNRATE, label='Unemployment Rate')
axes[0].plot(unemployment_US.index, result.level.smoothed, label='Random Walk')
axes[0].legend(loc='upper left')
axes[0].set(title='Level/Trend Component')
axes[1].set(title='AR Component')
axes[1].plot(unemployment_US.index, result.autoregressive.smoothed, label='AR')
axes[1].legend(loc='upper left')
fig.tight_layout()
plt.show()
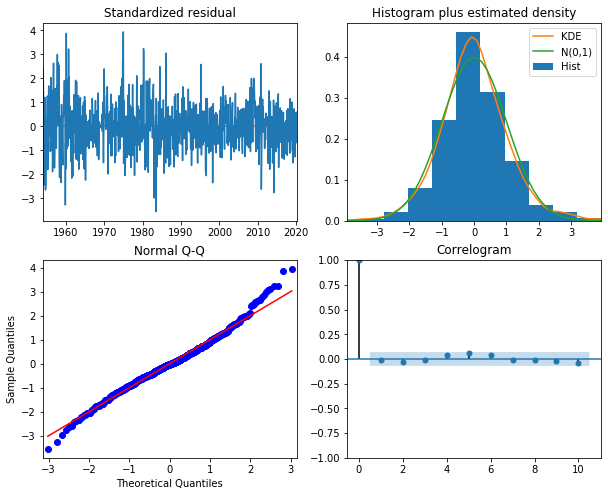
# 잔차진단
result.plot_diagnostics(figsize=(10,8))
plt.show()
Optimization terminated successfully.
Current function value: -0.324535
Iterations: 8
Function evaluations: 614
| Dep. Variable: | UNRATE | No. Observations: | 794 |
|---|---|---|---|
| Model: | random walk | Log Likelihood | 257.681 |
| + AR(4) | AIC | -503.362 | |
| Date: | Fri, 13 Mar 2020 | BIC | -475.307 |
| Time: | 23:32:27 | HQIC | -492.580 |
| Sample: | 01-01-1954 | ||
| - 02-01-2020 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2.level | 0.0172 | 0.003 | 6.277 | 0.000 | 0.012 | 0.023 |
| sigma2.ar | 0.0109 | 0.003 | 3.579 | 0.000 | 0.005 | 0.017 |
| ar.L1 | 1.0368 | 0.064 | 16.127 | 0.000 | 0.911 | 1.163 |
| ar.L2 | 0.4734 | 0.103 | 4.580 | 0.000 | 0.271 | 0.676 |
| ar.L3 | -0.3340 | 0.122 | -2.729 | 0.006 | -0.574 | -0.094 |
| ar.L4 | -0.1866 | 0.075 | -2.490 | 0.013 | -0.333 | -0.040 |
| Ljung-Box (Q): | 75.39 | Jarque-Bera (JB): | 45.00 |
|---|---|---|---|
| Prob(Q): | 0.00 | Prob(JB): | 0.00 |
| Heteroskedasticity (H): | 0.49 | Skew: | 0.25 |
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 4.06 |
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
확장 알고리즘 및 응용 예시¶
1) 확률적 변동성 모형 (Stochastic Volatility Model)
정적 변동성 모형: ARCH(Autoregressive conditional heteroskedasticity), GARCH(Generalized Autoregressive conditional heteroskedasticity)
정적 변동성 모형과 달리 변동성 자체를 하나의 독립적인 상태 변수로 가정
널리 사용되는 Heston 모형은 다음과 같이 분산(Variance) 상태 변수 \(\nu_t\)를 가지는 연속 시간 모형
\begin{align*} dS_t &= \mu S_t,dt + \sqrt{\nu_t} S_t,dW^S_t \ d\nu_t &= \kappa(\theta - \nu_t),dt + \xi \sqrt{\nu_t},dW^{\nu}_t \end{align*}
2) 히든 마코프 모형 (HMM: Hidden Markov Model)
상태 변수 \(x\) 값이 연속 확률변수가 아니라 1차원 이산 확률변수(Discrete Random Variable)인 경우 히든 마코프 모형이 됨
히든 마코프 모형의 상태 전이식은 다음과 같은 조건부 확률로 정의됨
주로 음성 처리에서 많이 사용되지만 경제학 분야에서도 구조적 변화에 의한 시계열 특성이 변화하는 경우에 사용됨
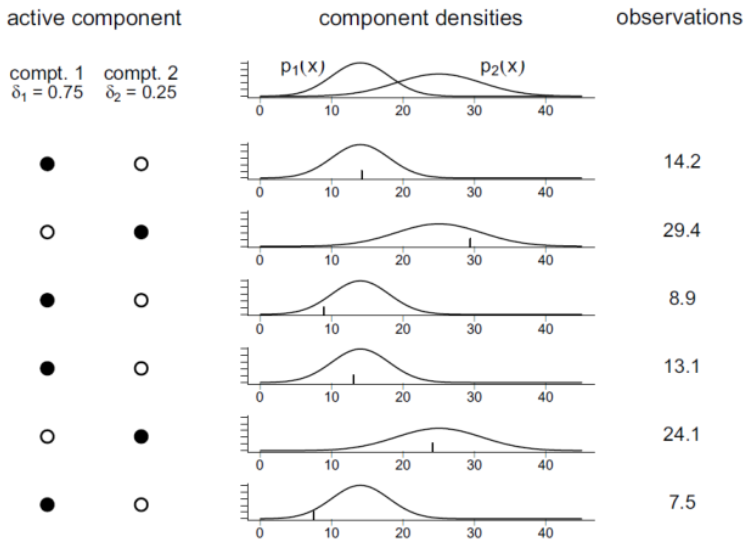
독립 혼합 모형(Independent Mixuture Model)
연속 확률변수임에도 단일 확률분포를 가지지 않고 복수의 확률분포를 가지는 경우, 독립적 이산 확률분포로 복수의 확률분포를 추정하는 모형 \begin{align*} p(y) &= \sum_{i=1}^m {P}(C=i)\cdot {P}(Y=y|C=i) \ &= \sum_{i=1}^m \delta_i p_i(y) \end{align*}
\(p(y)\): 전체 Independent Mixuture 분포
\(pi(y)\): Independent Mixuture 각 성분(Component)의 개별적인 연속 확률분포
\(\delta_i\): Mixing Parameter로 특정시간의 모든 성분 중 특정한 \(pi(y)\)가 선택될 확률(이산 확률 분포)
\(\sum \delta_i\): Mixing Parameter에 대한 확률 제한 조건
예시: 베르누이-정규 혼합모형(Binomial Normal-Mixture Model) - 베르누이 확률변수의 값에 따라 두개의 서로다른 연속정규분포 중 하나를 선택하는 확률분포
마코프 체인(Markov Chain)
마코프 체인(Markov Chain): 다음과 같은 특성을 가진 이산시간 확률 프로세스 \begin{align*} P(C_{t+1} \mid C_t, \cdots, C_1) = P(C_{t+1} \mid C_t) \end{align*}
전이확률(Transition Probability): \(t\)시간 동안 특정 상태 \(i\)에서 다른 상태 \(j\)로 전이할 확률 \begin{align*} \gamma_{ij}(t) = P(C_{s+t}=j|C_{s}=i) \end{align*}
전이행렬(Transition Matrix): 모든 상태조합에 대한 전이확률 \begin{align*} \Gamma(t) = { \gamma_{ij}(t) }, ;;; \Gamma = \Gamma(1) \end{align*}
체프먼-콜모고로프 방정식(Chapman-Kolmogorov Equation): 시간 \(t+u\)의 전이확률행렬은 시간\(t\)의 전이확률행렬과 시간 \(u\)의 전이확률행렬의 곱 \begin{align*} \Gamma(t+u) = \Gamma(t)\Gamma(u) \end{align*}
디코드(Decode): 관측된 HMM 모형의 연혹 확률변수 값으로 내부의 이산 확률변수 값을 추정하는 과정
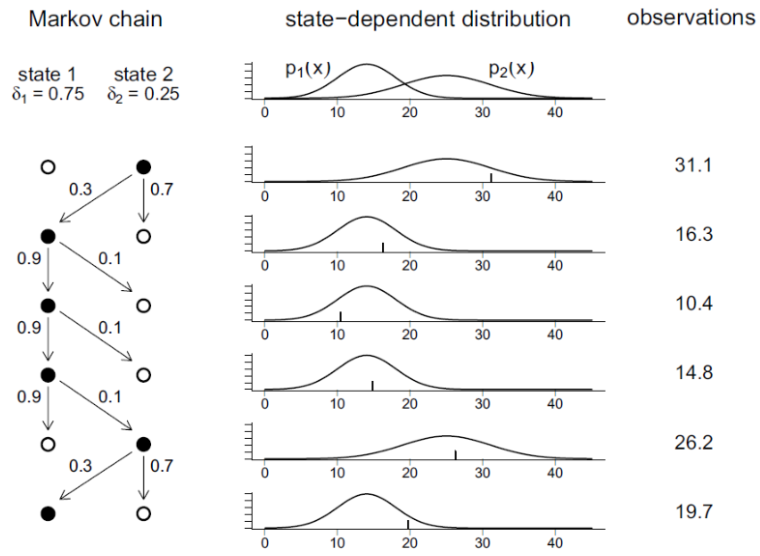
히든 마코프 모형(Hidden Markov Model)
독립 혼합 모형에서 연속 확률분포를 선택하는 이산확률과정 \(C_t\)가 마코프 체인이고 연속확률분포 \(Y_t\)가 그 시점의 이산 확률과정의 값에만 의존하는 모형
연속 확률 분포의 값 \(X_t\)만 측정 가능하고 이산 확률 과정의 값 \(C_t\)는 측정 불가 \begin{align*} P(C_t \mid |C_{t-1}, \cdots, C_1) = P(C_t \mid C_{t-1}) \ P(Y_t \mid Y_t, \cdots, Y_1, C_t, \cdots, C_1) = P(Y_t \mid C_t) \end{align*}
HMM 모듈 정리
from hmmlearn import hmm
클래스 이름 |
용도 |
|---|---|
GaussianHMM |
Hidden Markov Model with Gaussian emissions |
GMMHMM |
Hidden Markov Model with Gaussian mixture emissions |
MultinomialHMM |
Hidden Markov Model with multinomial (discrete) emissions |
GaussianHMM: 카테고리-다변수 정규분포 혼합 모형 시뮬레이션
출력모듈 |
설명 |
|---|---|
startprob_ |
초기 확률 벡터 |
transmat_ |
전이 확률 행렬 |
means_ |
정규 분포의 기댓값 벡터 |
covars_ |
정규 분포의 공분산 행렬 |
3) 칼만 필터
선형 동적 모형에 대한 필터링 문제와 스무딩 문제를 푸는 방법 중 가장 널리 쓰임
칼만 필터는 확률 변수의 분포를 갱신하는 베이지안 필터(Bayesian Filter)의 한 종류
가우시안 분포를 가지는 선형 시스템이라는 제약 조건을 훌륭하게 사용하여 상태 변수의 평균과 분산을 간단히 갱신하는 효율적 알고리즘 \begin{align*} \text{Main Equation} && \alpha_t &= T_t \alpha_{t-1} + c_t + R_t \eta_t \ && y_t &= Z_t \alpha_t + d_t + \varepsilon_t \ \text{where} && & \text{\(\alpha_t\): State Vector} \ && & \text{\(T_t\): Transition Matrix} \ && & \text{\(c_t\): State Intercept Vector} \ && & \text{\(R_t\): Selection Matrix} \ && & \text{\(\eta_t \sim N(0, Q_t)\): Innovation Process Vector} \ && & \text{\(Q_t\): State Covariance Matrix} \ && & \text{\(y_t\): Observation Vector} \ && & \text{\(Z_t\): Design Matrix} \ && & \text{\(d_t\): Observation Intercept Vector} \ && & \text{\(\epsilon_t \sim N(0, H_t)\): Observation Error Vector} \ && & \text{\(H_t\): Observation Covariance Matrix} \ \end{align*}
from statsmodels.tsa.statespace.kalman_filter import KalmanFilter
model = KalmanFilter(yt, k_states=1, transition=[[1]], selection=[[1]],
state_cov=[[10]], design=[[1]], obs_cov=[[100]])
입력옵션 |
설명 |
|---|---|
k_endog |
정수 혹은 배열. 배열인 경우에는 칼만필터를 적용할 실제 시계열 자료. 정수인 경우에는 출력 변수의 수 |
k_states |
정수. 상태 변수의 수 |
k_posdef |
(옵션) 정수. 출력 잡음의 공분산 중 양 한정(Positive Definite)을 보장하는 차원의 수. 디폴트는 k_states |
transition |
(옵션) 상태 전이 행렬(Transition Matrix). 디폴트는 0 |
state_intercept |
(옵션) 상태 전이식의 절편(Intercept for the Transition Equation). 디폴트는 0 |
selection |
(옵션) 이노베이션 과정에 대한 선택 행렬(Selection Matrix). 디폴트는 0 |
state_cov |
(옵션) 이노베이션 과정의 공분산 행렬. 디폴트는 0 |
design |
(옵션) 설계 행렬(Design Matrix). 디폴트는 0 |
obs_intercept |
(옵션) 관측식의 절편(Intercept for the Observation Equation). 디폴트는 0 |
obs_cov |
(옵션) 관측 행렬의 공분산 행렬. 디폴트는 0 |
initial_state |
(옵션) 배열. 초기 상태 변수 값 |
initialization |
(옵션) 다음 문자열 중 하나 {approximate_diffuse, stationary, known} (옵션) 상태 변수 초기화 방법 |
initial_variance |
(옵션) 실수. 초기화 방법이 Approximate_diffuse 일 경우의 초기 분산 값. 디폴트는 1e6 |
initial_state_cov |
(옵션) 배열. 초기화 방법이 Known 일 경우 사용하는 분산 행렬 |
nobs |
(옵션) 정수. k_endog가 정수인 경우에 시계열 자료의 길이를 표시 |
loglikelihood_burn |
(옵션) 정수. Log-likelihood를 기록하지 않는 Burn-in 구간의 길이. 디폴트는 0 |
tolerance |
(옵션) 실수. 상태변수의 수렴 기준. 디폴트는 1e-19 |
출력모듈 |
설명 |
|---|---|
simulate |
모수가 모두 충족된 경우 시뮬레이션 수행 |
initialize_known |
초기 상태 생성 (상태값을 아는 경우) |
initialize_stationary |
초기 상태 생성 (정상 상태) |
initialize_approximate_diffuse |
초기 상태 생성 |
filter |
필터링. FilterResults 객체 출력 |
4) 마코프 체인 몬테카를로 (MCMC: Markov Chain Monte Carlo)
상태 공간 모형의 확률 분포가 가우시안 정규 분포가 아니거나 정확한 분포의 수식을 알 수 없을 때 주로 활용
MCMC 방법은 특정한 마코프 체인 확률 과정을 사용하여 생성한 시뮬레이션을 통해 분포의 형상을 추정
5) 응용 사례
기존 ARMA 모형에서 다루기 힘든 문제들을 해결하는데 도움
시계열의 구조적 모형(structural model)
일부 누락된 데이터(missing data)가 있는 경우
시간에 따라 모형 계수가 변화(time-varing or switching)하는 경우
변수의 분포가 정규 분포가 아닌 경우
실습: HMM 데이터생성 및 이해¶
# import numpy as np
# from hmmlearn import hmm
# import seaborn as sns
# import matplotlib.pyplot as plt
# # 데이터 생성
# np.random.seed(3)
# model = hmm.GaussianHMM(n_components=2, covariance_type="diag")
# model.startprob_ = np.array([0.9, 0.1])
# model.transmat_ = np.array([[0.95, 0.05], [0.15, 0.85]])
# model.means_ = np.array([[1.0], [-3.0]])
# model.covars_ = np.array([[15.0], [40.0]])
# X, Z = model.sample(500)
# # 데이터 시각화
# plt.figure(figsize=(10,6))
# sns.distplot(X)
# plt.show()
# plt.figure(figsize=(10,6))
# plt.subplot(311)
# plt.plot(X)
# plt.title("random variable")
# plt.subplot(312)
# plt.plot(Z)
# plt.title("discrete state")
# plt.subplot(313)
# plt.plot((1 + 0.01*X).cumprod())
# plt.title("X cumulated")
# plt.tight_layout()
# plt.show()
# # HMM 모델링
# fit = hmm.GaussianHMM(n_components=2, n_iter=len(X)).fit(X)
# Z_hat = fit.decode(X)[1]
# X_cum = (1 + 0.01*X).cumprod()
# X_cum_hat = X_cum.copy()
# X_cum_hat[Z_hat == 0] = np.nan
# # Generator 시각화
# plt.figure(figsize=(10,6))
# plt.subplot(211)
# plt.plot(X_cum, lw=5)
# plt.plot(X_cum_hat, 'r-', lw=5)
# plt.title("X cumulated")
# plt.subplot(212)
# plt.plot(Z, 'bo-')
# plt.plot(Z_hat, 'ro-')
# plt.title("discrete state")
# plt.tight_layout()
# plt.show()
실습: Kalman Filter 데이터생성 및 이해¶
\begin{align*} \mu_t &= \mu_{t-1} + w_t,;;; &w_t \sim N(\mu=0, \sigma^2=10) \ Y_{t} &= \mu_{t} + v_t,;;; &v_t \sim N(\mu=0, \sigma^2=100) \ \end{align*}
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.kalman_filter import KalmanFilter
# 데이터 생성
np.random.seed(123)
model_generator = KalmanFilter(k_endog=1, k_states=1,
transition=[[1]], selection=[[1]], state_cov=[[10]],
design=[[1]], obs_cov=[[100]])
y_gener, x_gener = model_generator.simulate(100)
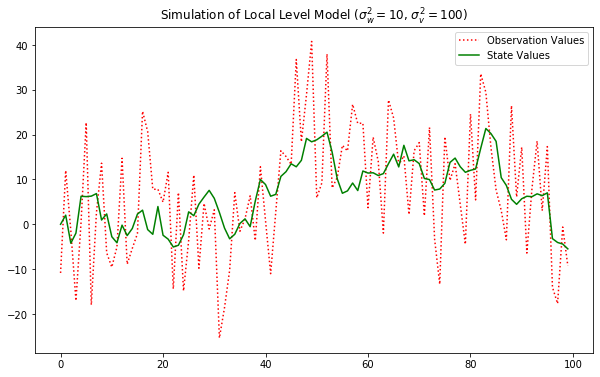
# 데이터 생성
plt.figure(figsize=(10,6))
plt.plot(y_gener, 'r:', label="Observation Values")
plt.plot(x_gener, 'g-', label="State Values")
plt.legend()
plt.title("Simulation of Local Level Model ($\sigma_w^2 = 10$, $\sigma_v^2 = 100$)")
plt.show()
# Kalman Filter 모델링
fit = KalmanFilter(y_gener, k_states=1,
transition=[[1]], selection=[[1]], state_cov=[[10]],
design=[[1]], obs_cov=[[100]])
fit.initialize_known([0], [[1]])
result = fit.filter()
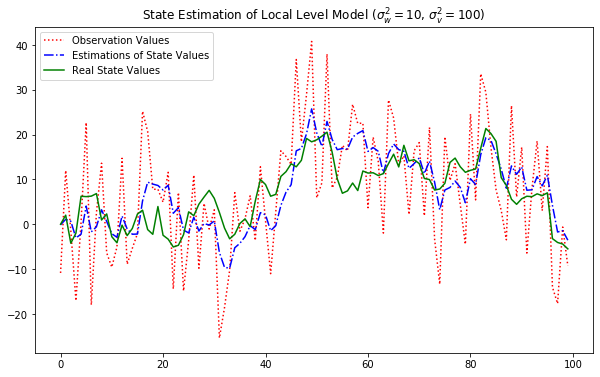
# 추정 시각화
plt.figure(figsize=(10,6))
plt.plot(fit.obs[0], 'r:', label="Observation Values")
plt.plot(result.filtered_state[0], "b-.", label="Estimations of State Values")
plt.plot(x_gener, "g-", label="Real State Values")
plt.legend()
plt.title("State Estimation of Local Level Model ($\sigma_w^2 = 10$, $\sigma_v^2 = 100$)")
plt.show()
다변량 시계열 알고리즘¶
필요성:
단변량 시계열(Simple/Multiple포함)은 종속변수(\(Y_t\))가 독립변수들에만! 영향을 받는다는 큰 가정 존재
현실적으론 종속변수와 독립변수는 상호 영향을 주고받음
예시: 개인 소득과 지출 중 어떤게 Y로 적합한가?라는 질문은 왜 하지 않는가?
2차원(소득과 지출 모두를 종속변수) 과거1시점까지만을 고려하는 백터자기회귀 알고리즘
\begin{align*} \text{Equation of VAR(1)} && Y_{[t]} &= A Y_{[t-1]} + \epsilon_{[t]} \ \text{where} && Y_{[t]} &= \begin{bmatrix} Y_{1t} \ Y_{2t} \end{bmatrix}, A = \begin{bmatrix} \phi_{11} \phi_{12} \ \phi_{21} \phi_{22} \end{bmatrix}, Y_{[t-1]} = \begin{bmatrix} Y_{1t-1} \ Y_{2t-1} \end{bmatrix}, \ && \epsilon_{[t]} &= \begin{bmatrix} e_{1t} \ e_{2t} \end{bmatrix} \sim N(0, \textstyle \sum_{\epsilon_{[t]}}) \ \text{Each Equation of VAR(1)} && Y_{1t} &= \phi_{11} Y_{1t-1} + \phi_{12} Y_{2t-1} + e_{1t} \ && Y_{2t} &= \phi_{21} Y_{1t-1} + \phi_{22} Y_{2t-1} + e_{2t} \ \end{align*}
벡터자기회귀 모형(Vector Autoregressive Model)¶
1) VAR 알고리즘:
단변량 시계열과 같이 평균 벡터와 공분산 벡터가 시차 \(l\)에만 의존하고 각각의 절대위치에 독립적이면 정상성(Stationary) 시계열
\begin{align*} \text{Generalized Equation of VAR(1)} && Y_{[t]} &= A_1 Y_{[t-1]} + e_t \ \text{where} && Y_{[t]} &= \begin{bmatrix} Y_{1t} \ Y_{2t} \ \vdots \ Y_{kt} \end{bmatrix}, A_1 = \begin{bmatrix} \phi_{11}^1 \phi_{12}^1 \cdots \phi_{1k}^1 \ \phi_{21}^1 \phi_{22}^1 \cdots \phi_{2k}^1 \ \vdots \ \phi_{k1}^1 \phi_{k2}^1 \cdots \phi_{kk}^1 \end{bmatrix}, Y_{[t-1]} = \begin{bmatrix} Y_{1t-1} \ Y_{2t-1} \ \vdots \ Y_{kt-1} \end{bmatrix}, \ && \epsilon_{[t]} &= \begin{bmatrix} e_{1t} \ e_{2t} \ \vdots \ e_{kt} \end{bmatrix} \sim N(0, \textstyle \sum_{\epsilon_{[t]}}) \ \text{Each Equations} && Y_{1t} &= \phi_{11}^1 Y_{1t-1} + \phi_{12}^1 Y_{2t-1} + \cdots + \phi_{1k}^1 Y_{kt-1} + e_{1t} \ && Y_{2t} &= \phi_{21}^1 Y_{1t-1} + \phi_{22}^1 Y_{2t-1} + \cdots + \phi_{2k}^1 Y_{kt-1} + e_{2t} \ && & \vdots \ && Y_{kt} &= \phi_{k1}^1 Y_{1t-1} + \phi_{k2}^1 Y_{2t-1} + \cdots + \phi_{kk}^1 Y_{kt-1} + e_{kt} \ \end{align*}
\begin{align*} \text{Generalized Equation of VAR(2)} && Y_{[t]} &= A_1 Y_{[t-1]} + A_2 Y_{[t-2]} + e_t \ \text{where} && Y_{[t]} &= \begin{bmatrix} Y_{1t} \ Y_{2t} \ \vdots \ Y_{kt} \end{bmatrix}, A_1 = \begin{bmatrix} \phi_{11}^1 \phi_{12}^1 \cdots \phi_{1k}^1 \ \phi_{21}^1 \phi_{22}^1 \cdots \phi_{2k}^1 \ \vdots \ \phi_{k1}^1 \phi_{k2}^1 \cdots \phi_{kk}^1 \end{bmatrix}, Y_{[t-1]} = \begin{bmatrix} Y_{1t-1} \ Y_{2t-1} \ \vdots \ Y_{kt-1} \end{bmatrix}, \ && A_2 &= \begin{bmatrix} \phi_{11}^2 \phi_{12}^2 \cdots \phi_{1k}^2 \ \phi_{21}^2 \phi_{22}^2 \cdots \phi_{2k}^2 \ \vdots \ \phi_{k1}^2 \phi_{k2}^2 \cdots \phi_{kk}^2 \end{bmatrix}, Y_{[t-2]} = \begin{bmatrix} Y_{1t-2} \ Y_{2t-2} \ \vdots \ Y_{kt-2} \end{bmatrix}, \ && \epsilon_{[t]} &= \begin{bmatrix} e_{1t} \ e_{2t} \ \vdots \ e_{kt} \end{bmatrix} \sim N(0, \textstyle \sum_{\epsilon_{[t]}}) \ \text{Each Equations} && Y_{1t} &= \phi_{11}^1 Y_{1t-1} + \phi_{12}^1 Y_{2t-1} + \cdots + \phi_{1k}^2 Y_{kt-2} + \phi_{11}^2 Y_{1t-2} + \phi_{12}^2 Y_{2t-2} + \cdots + \phi_{1k}^2 Y_{kt-2} + e_{1t} \ && Y_{2t} &= \phi_{21}^1 Y_{1t-1} + \phi_{22}^1 Y_{2t-1} + \cdots + \phi_{2k}^1 Y_{kt-1} + \phi_{21}^2 Y_{1t-2} + \phi_{22}^2 Y_{2t-2} + \cdots + \phi_{2k}^2 Y_{kt-2} + e_{2t} \ && & \vdots \ && Y_{kt} &= \phi_{k1}^1 Y_{1t-1} + \phi_{k2}^1 Y_{2t-1} + \cdots + \phi_{kk}^1 Y_{kt-1} + \phi_{k1}^2 Y_{1t-2} + \phi_{k2}^2 Y_{2t-2} + \cdots + \phi_{kk}^2 Y_{kt-2} + e_{kt} \ \end{align*}
\begin{align*} \text{Generalized Equation of VAR(p)} && Y_{[t]} &= A_1 Y_{[t-1]} + A_2 Y_{[t-2]} + \cdots + A_p Y_{[t-p]} + \epsilon_{[t]} \ \text{Mean} && \mu_{[t]} &= \text{E}(Y_{[t]}) = \begin{bmatrix} \text{E}(Y_{1t}) \ \text{E}(Y_{2t}) \ \vdots \ \text{E}(Y_{kt}) \end{bmatrix} = \begin{bmatrix} \mu_{1} \ \mu_{2}\ \vdots \ \mu_{k} \end{bmatrix} \ \text{Covariance} && \Gamma(l) &= \text{E}[(Y_{[t]} − \mu_{[t]})(Y_{[t]} − \mu_{[t]})^T ] \ && &= \begin{bmatrix} \text{E}[(Y_{1t} − \mu_1)^2] & \text{E}[(Y_{1t} − \mu_1)(Y_{2t} − \mu_2)] & \cdots & \text{E}[(Y_{1t} − \mu_1)(Y_{kt} − \mu_k)] \ \text{E}[(Y_{2t} − \mu_2)(Y_{1t} − \mu_1)] & \text{E}[(Y_{2t} − \mu_2)^2] & \cdots & \text{E}[(Y_{2t} − \mu_2)(Y_{kt} − \mu_k)] \ \vdots & \vdots & \ddots & \vdots \ \text{E}[(Y_{kt} − \mu_k)(Y_{1t} − \mu_1)]& \text{E}[(Y_{kt} − \mu_k)(Y_{2t} − \mu_2)] & \cdots & \text{E}[(Y_{kt} − \mu_k)^2] \ \end{bmatrix} \ \text{Covariance Diagonal} && D &= \text{diag}(\sqrt{\Gamma_{11}}, \cdots, \sqrt{\Gamma_{kk}}) \ \text{Cross-correlation Matrix} && \rho(l) &= D^{−1}\Gamma(l)D^{−1} \ \end{align*}
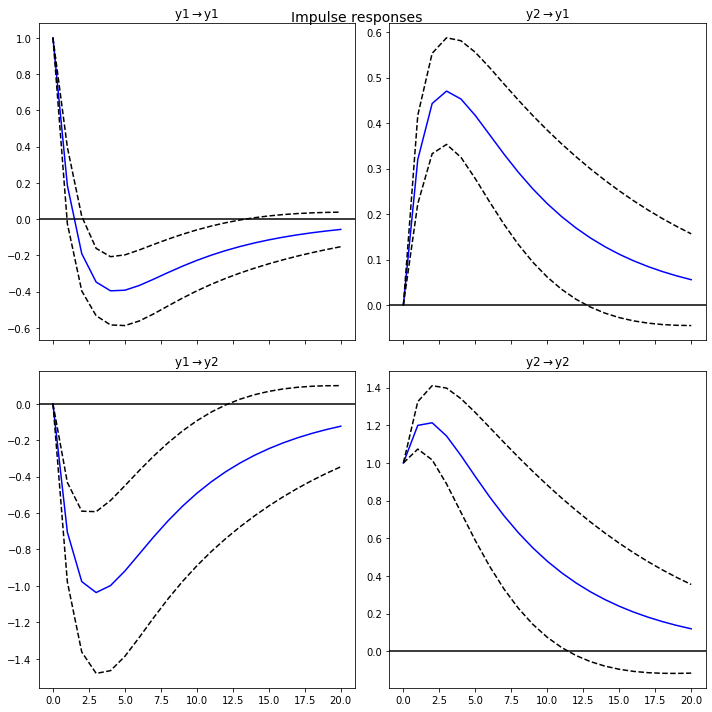
2) 임펄스 응답 함수(Impulse Response Function):
VAR 모형은 여러개의 시계열 상호상관관계를 기반으로 각각의 변수가 다른 변수에 어떤 영향을 주는지 임펄스 반응 함수로 알 수 있음
임펄스(Impulse): 어떤 시계열이 \(t=0\) 일 때 1이고, \(t<0\) 또는 \(t>1\) 일 때 0인 것
임펄스 반응 함수(Impulse Response Function): 임펄스 형태의 시계열이 다른 시계열에 미치는 영향을 시간에 따라 표시
VAR 모듈 정리¶
클래스 이름 |
용도 |
|---|---|
VARProcess |
미리 정해진 계수를 가진 \(VAR\) 모형 |
VAR |
주어진 자료의 계수를 추정하기 위한 \(VAR\) 모형 |
VARResults |
주어진 자료로 추정된 \(VAR\) 모형 |
1) VARProcess
출력모듈 |
설명 |
|---|---|
acf([nlags]) |
이론적인 공분산 함수(autocovariance function) 계산 |
acorr([nlags]) |
이론적인 자기상관계수 함수(autocorrelation function) 계산 |
forecast(y, steps) |
최소자승 미래 예측값 계산 |
forecast_cov(steps) |
미래 예측 오차 공분산 행렬 계산 |
forecast_interval(y, steps[, alpha]) |
미래 구간 예측 |
get_eq_index(name) |
지정한 이름ㄹ 가진 정수 위치 반환 |
is_stable([verbose]) |
안정성 계산 |
long_run_effects() |
임펄스 함수의 장기 효과 계산 |
ma_rep([maxn]) |
\(MA(\infty\)) 계수 행렬 계산 |
mean() |
기댓값 |
mse(steps) |
이론적인 미래예측 오차 행렬 계산 |
plot_acorr([nlags, linewidth]) |
이론적인 자기상관계수 함수 행렬 플롯 |
plotsim([steps]) |
시물레이션 플롯 |
2) VAR
출력모듈 |
설명 |
|---|---|
endog |
원자료 |
endog_names |
원자료 변수명 |
3) VARResults
출력모듈 |
설명 |
|---|---|
model |
추정 자료와 모형 차수 등을 가진 VAR 클래스 객체 |
k_ar |
AR 차수 |
coefs |
추정된 AR 계수 |
intercept |
추정된 trend constant |
params |
추정된 전체 계수 (trend constant 포함) |
bse |
추정된 전체 계수의 표준 오차 |
tvalues |
추정된 계수의 t statistics |
pvalues |
추정된 계수의 t statistics에 대한 p value |
llf |
Log Likelihood 값 |
aic |
AIC 값 |
bic |
AIC 값 |
hqic |
HQIC 값 |
fittedvalues |
추정 모형에 의한 예측값 |
resid |
추정 모형에 의한 잔차항(Residuals) |
sigma_u |
추정 모형에 의한 잔차항의 분산 |
실습: VAR 데이터생성 및 이해¶
\begin{align*} \text{Example of VAR(1)} && Y_{1t} &= 5 + 0.2 Y_{1t-1} + 0.3 Y_{2t-1} + e_{1t} \ && Y_{2t} &= 3 - 0.6 Y_{1t-1} + 1.1 Y_{2t-1} + e_{2t} \ \end{align*}
import numpy as np
import matplotlib.pyplot as plt
import statsmodels
import statsmodels.api as sm
# 차수 입력
intercept = np.array([5, 3])
matrix_A = np.array([[[0.2, 0.3], [-0.6, 1.1]]])
residual_covariance = np.array([[1, 0.8],[0.8, 2]])
# VAR 데이터 생성
fit = statsmodels.tsa.vector_ar.var_model.VARProcess(matrix_A, intercept, residual_covariance)
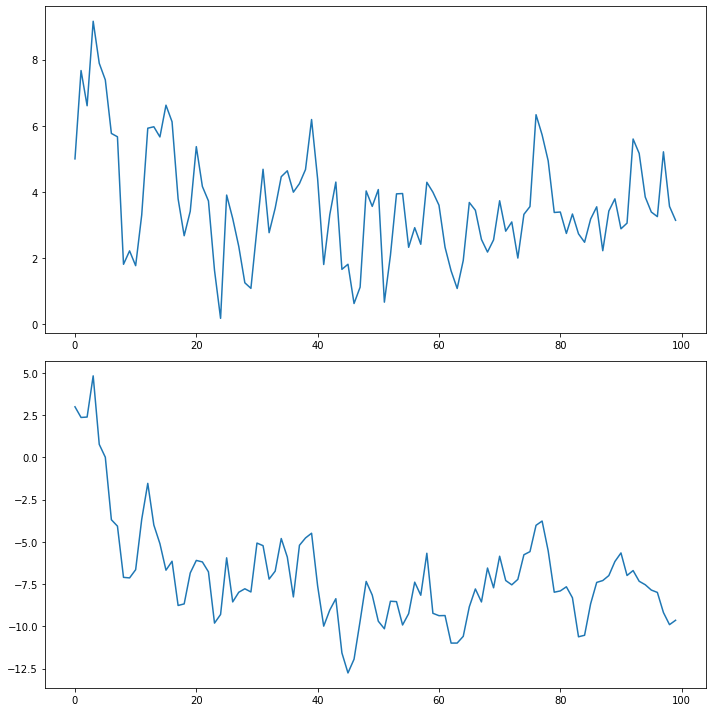
## 시뮬레이션 시각화1
simul_num = 100
fit.plotsim(steps=simul_num, seed=123)
plt.tight_layout()
plt.show()
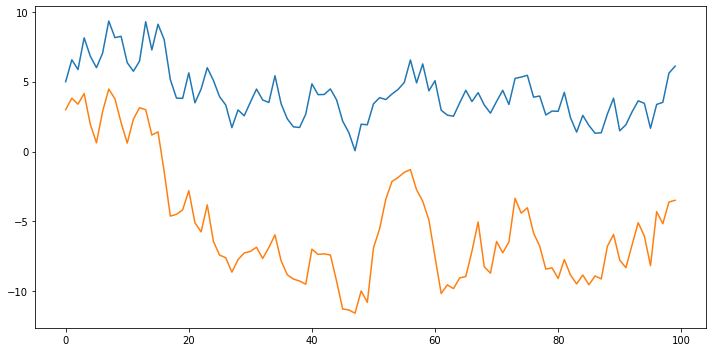
## 시뮬레이션 시각화2
simul_num = 100
simul_values = statsmodels.tsa.vector_ar.util.varsim(fit.coefs, fit.intercept, fit.sigma_u, steps=simul_num)
plt.figure(figsize=(10,5))
plt.plot(simul_values)
plt.tight_layout()
plt.show()
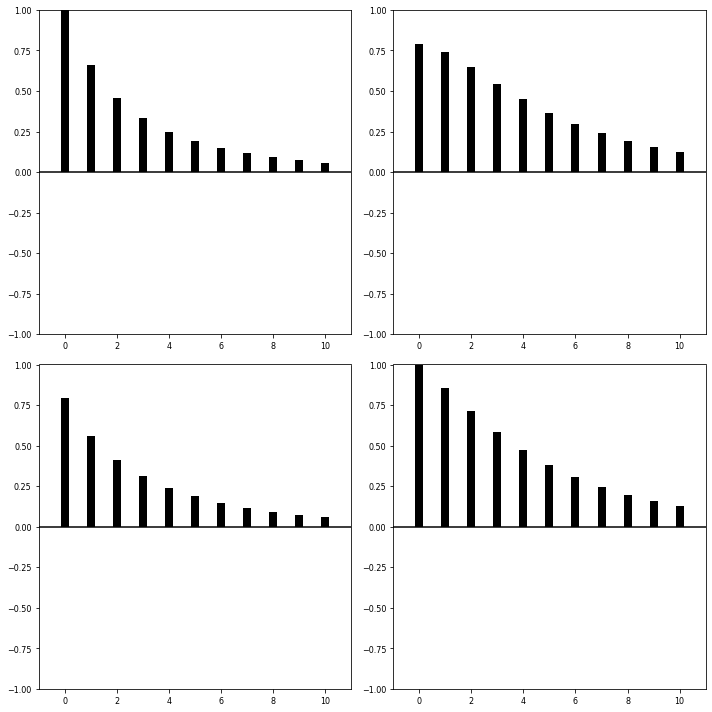
## ACF 시각화
fit.plot_acorr()
plt.tight_layout()
plt.show()
# VAR 모형적합
fit = sm.tsa.VAR(simul_values).fit()
display(fit.summary())
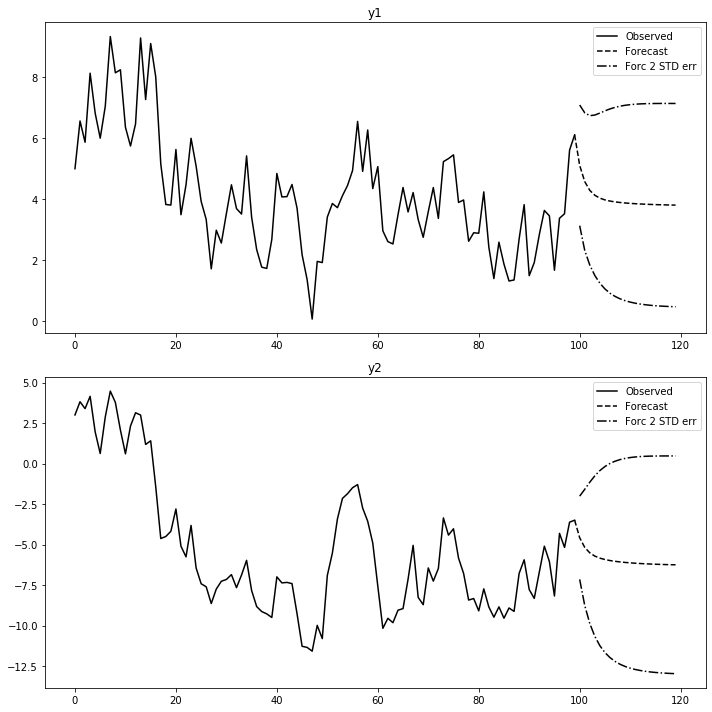
# 예측 및 시각화
forecast_num = 20
pred_var = fit.forecast(fit.model.endog[-1:], steps=forecast_num)
pred_var_ci = fit.forecast_interval(fit.model.endog[-1:], steps=forecast_num)
fit.plot_forecast(forecast_num)
plt.tight_layout()
plt.show()
# 임펄스반응함수 추정
fit.irf(forecast_num).plot()
plt.tight_layout()
plt.show()
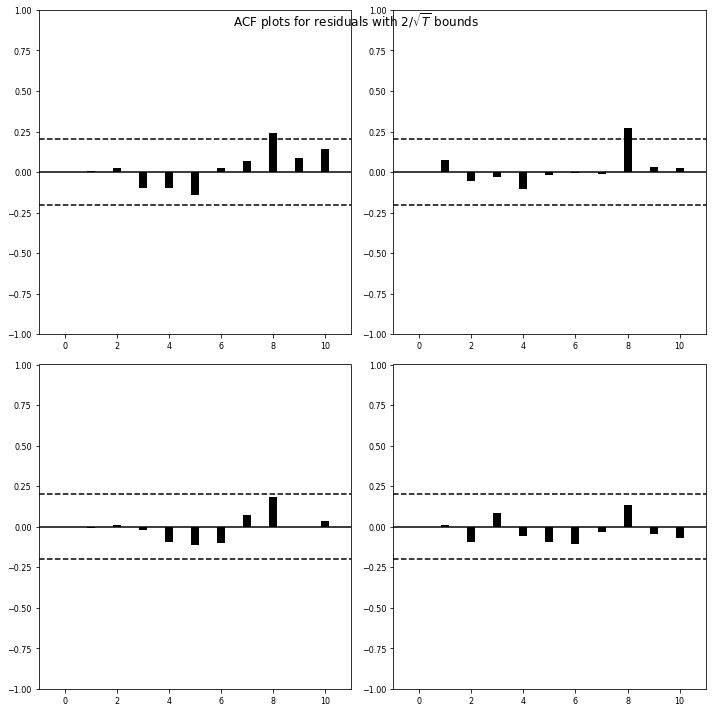
# 잔차진단
fit.plot_acorr()
plt.tight_layout()
plt.show()
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Fri, 13, Mar, 2020
Time: 23:32:41
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: 0.325657
Nobs: 99.0000 HQIC: 0.232012
Log likelihood: -283.284 FPE: 1.18343
AIC: 0.168377 Det(Omega_mle): 1.11484
--------------------------------------------------------------------
Results for equation y1
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 5.094687 0.696008 7.320 0.000
L1.y1 0.185511 0.107543 1.725 0.085
L1.y2 0.319971 0.049597 6.451 0.000
========================================================================
Results for equation y2
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 3.922002 0.901511 4.350 0.000
L1.y1 -0.704885 0.139297 -5.060 0.000
L1.y2 1.199559 0.064241 18.673 0.000
========================================================================
Correlation matrix of residuals
y1 y2
y1 1.000000 0.604778
y2 0.604778 1.000000
실습: 거시경제 VAR 모형화 및 해석¶
데이터설명: 링크
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels
import statsmodels.api as sm
# 데이터 로딩
raw = sm.datasets.macrodata.load_pandas().data
dates_info = raw[['year', 'quarter']].astype(int).astype(str)
raw.index = pd.DatetimeIndex(sm.tsa.datetools.dates_from_str(dates_info['year'] + 'Q' + dates_info['quarter']))
raw_use = raw.iloc[:,2:5]
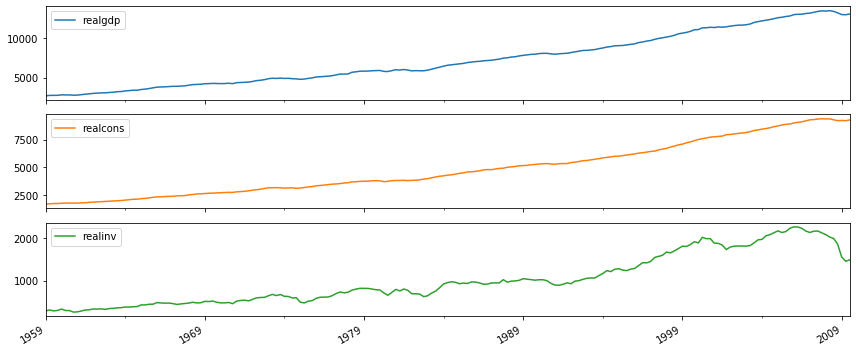
# 데이터 시각화
raw_use.plot(subplots=True, figsize=(12,5))
plt.tight_layout()
plt.show()
raw_use.diff(1).dropna().plot(subplots=True, figsize=(12,5))
plt.tight_layout()
plt.show()
# VAR 모형적합
raw_use_return = raw_use.diff(1).dropna()
fit = sm.tsa.VAR(raw_use_return).fit(maxlags=2)
display(fit.summary())
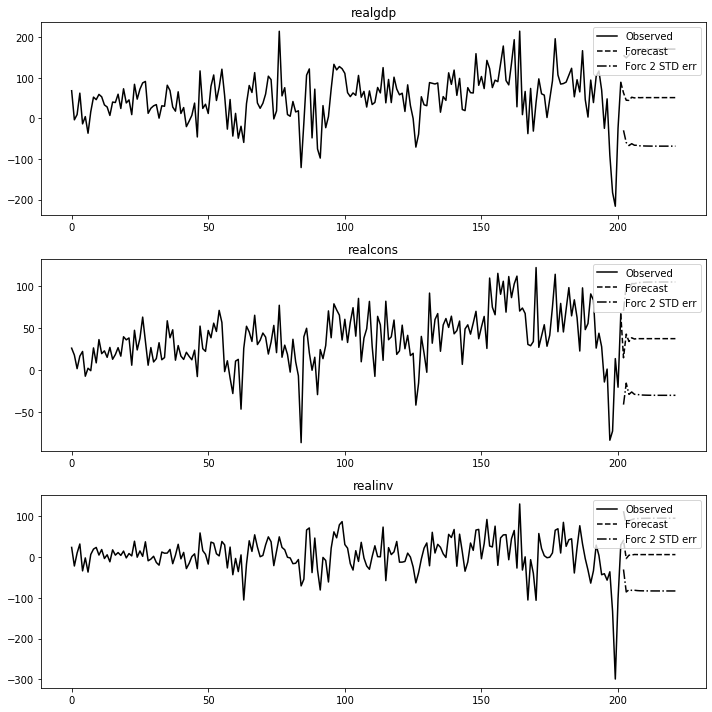
# # 예측 및 시각화
forecast_num = 20
# pred_var = fit.forecast(fit.model.endog[-1:], steps=forecast_num)
# pred_var_ci = fit.forecast_interval(fit.model.endog[-1:], steps=forecast_num)
fit.plot_forecast(forecast_num)
plt.tight_layout()
plt.show()
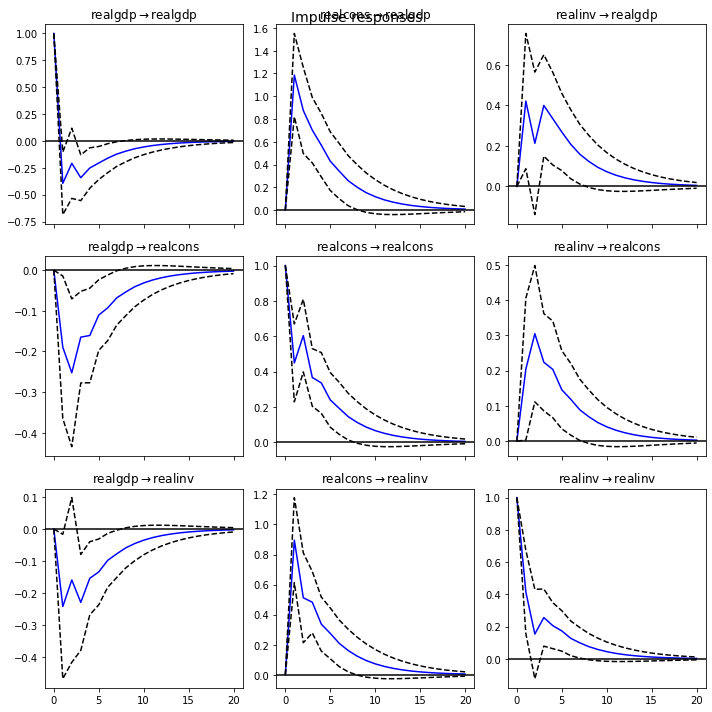
# 임펄스반응함수 추정
fit.irf(forecast_num).plot()
plt.tight_layout()
plt.show()
# 잔차진단
fit.plot_acorr()
plt.tight_layout()
plt.show()
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Fri, 13, Mar, 2020
Time: 23:32:48
--------------------------------------------------------------------
No. of Equations: 3.00000 BIC: 20.5675
Nobs: 200.000 HQIC: 20.3614
Log likelihood: -2852.49 FPE: 6.05346e+08
AIC: 20.2212 Det(Omega_mle): 5.45987e+08
--------------------------------------------------------------------
Results for equation realgdp
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 10.308143 6.425207 1.604 0.109
L1.realgdp -0.394370 0.148481 -2.656 0.008
L1.realcons 1.185980 0.186610 6.355 0.000
L1.realinv 0.421263 0.170349 2.473 0.013
L2.realgdp -0.036990 0.154523 -0.239 0.811
L2.realcons 0.432912 0.211433 2.048 0.041
L2.realinv -0.038513 0.172158 -0.224 0.823
==============================================================================
Results for equation realcons
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 21.101498 3.871854 5.450 0.000
L1.realgdp -0.189663 0.089475 -2.120 0.034
L1.realcons 0.448795 0.112452 3.991 0.000
L1.realinv 0.204550 0.102653 1.993 0.046
L2.realgdp -0.192664 0.093116 -2.069 0.039
L2.realcons 0.443486 0.127410 3.481 0.000
L2.realinv 0.208133 0.103743 2.006 0.045
==============================================================================
Results for equation realinv
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const -18.677662 4.969904 -3.758 0.000
L1.realgdp -0.241467 0.114850 -2.102 0.036
L1.realcons 0.895484 0.144343 6.204 0.000
L1.realinv 0.415102 0.131765 3.150 0.002
L2.realgdp 0.016095 0.119523 0.135 0.893
L2.realcons 0.024955 0.163543 0.153 0.879
L2.realinv -0.099367 0.133164 -0.746 0.456
==============================================================================
Correlation matrix of residuals
realgdp realcons realinv
realgdp 1.000000 0.507486 0.674775
realcons 0.507486 1.000000 -0.078787
realinv 0.674775 -0.078787 1.000000

그래인저 인과관계 모형(Granger Causality Model)¶
인과관계? 상관관계?¶
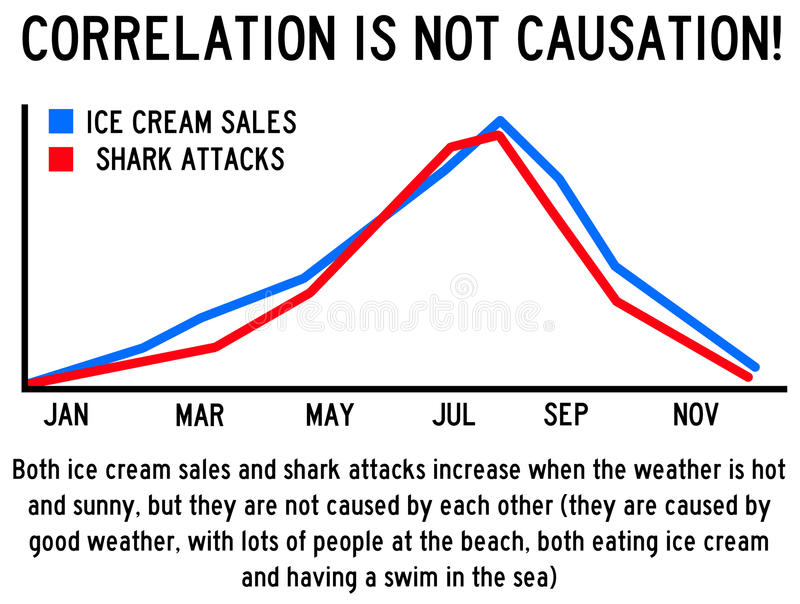
Spurious Regression
“\(X\)와 \(Y\)가 관련(인과관계)이 없거나 논리적인 스토리가 없음에도 단순하게 상관성이 높다라는 공격”
지나치게 데이터에 집착할 필요도 없고, 데이터분석은 정말 어려운 작업
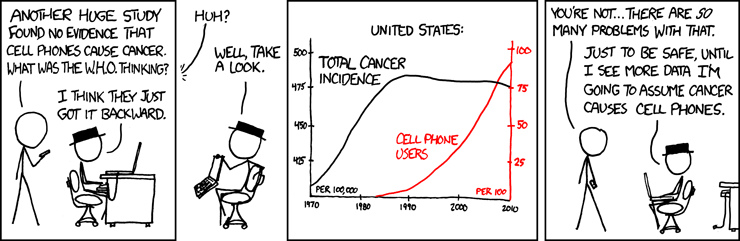
“\(X\) 다음에 \(Y\)가 일어났으므로 \(X\)가 \(Y\)의 원인이라는, 마치 시간순서가 인과관계를 담보할 것이라는 결과오류”
징크스: 머리를 염색했더니 시험점수가 100점이 나오더라?
오버피팅(Overfitting): 인과관계가 있는 데이터에서 샘플(Train) 데이터에 치우쳐버린 모델
Post Hoc Fallacy: 아무런 인과관계가 없는(상관관계는 높더라도) 데이터로 만든 모델
Granger Causality 이해¶
“어떤 현상의 예측에 있어 다른 정보를 이용하는 것이 얼마나 유의미한지 나타내는 척도”
추론불가한 문제: “닭이 먼저인가 달걀이 먼저인가?” (인과관계)
추론가능한 문제: “닭과 달걀의 생성순서 별 서로의 영향력은 어떤가?” (Granger 인과관계)
필요성: - 회귀분석에서 독립변수와 종속변수는 경제이론에 의해 이미 결정된 것으로 간주하고 인과관계 확인 - 원인과 결과가 불분명한 경우 함수관계에 대한 명확한 결정은 현실적으로 어려움
예시: - 닭과 달걀의 생산량의 인과관계 - 단기금리와 중기금리와의 인과관계 - 강수량과 동물원방문객수의 인과관계 - 급여인상액과 소비금액의 인과관계 - 어떤 회사의 광고비지출액와 매출액의 인과관계 - 강수량과 인터넷사용량의 인과관계 - 어떤 광고캠페인의 수치형 설정조건과 클릭수와 인과관계
모형의 전재: 과거의 사건은 현재의 사건을 유발할 수 있지만 미래의 사건은 현재의 사건을 유발할 수 없다
정상성: 정상성 데이터를 가정하므로 독립변수(\(X\))와 종속변수(\(Y\))는 모두 정상성 상태여야 함 (비정상 데이터기반 결과는 오해석 여지가 많음)
입력시차: 입력변수로 시차(Lagged) 적용된 변수를 반영해야 하며, 예상되는 시차가 \(N\)이라면, \(1\)부터 \(N\)까지의 시차 모두를 입력변수로 사용해야 함
최종시차: 예상시차 \(N\)에 매우 민감하므로 적합한 길이를 선택해야 함
통상 연 환산빈도의 2~3배까지: 연별 자료시 2, 분기별 자료시 8, 월별 자료시 24)
\(F\)검정통계량의 유의한 변화에 의해 결정
검정방향: 독립변수와 종속변수의 양방향 관련성 비교가 필요하기에 총2회의 검정을 수행해야 함
\(X \implies Y\) 1회: \(X\)가 \(Y\)에 인과영향인지 테스트 (\(\beta_j = 0\) 여부 확인, \(\epsilon_{XY}\) 분산 감소정도 확인) \begin{align*} \text{Just use Y} && Y_{t} &= \mu_t + \displaystyle \sum_{i=1}^{\infty} \alpha_i Y_{t-i} + \epsilon_{Y} \ \text{Use X and Y} && Y_{t} &= \mu_t + \displaystyle \sum_{i=1}^{\infty} \alpha_i Y_{t-i} + \displaystyle \sum_{j=1}^{\infty} \beta_j X_{t-j} + \epsilon_{XY} \ \end{align*}
\(Y \implies X\) 1회: \(Y\)가 \(X\)에 인과영향인지 테스트 (\(\beta_j = 0\) 여부 확인, \(\epsilon_{YX}\) 분산 감소정도 확인) \begin{align*} \text{Just use X} && X_{t} &= \mu_t + \displaystyle \sum_{i=1}^{\infty} \alpha_i X_{t-i} + \epsilon_{X} \ \text{Use X and Y} && X_{t} &= \mu_t + \displaystyle \sum_{i=1}^{\infty} \alpha_i X_{t-i} + \displaystyle \sum_{j=1}^{\infty} \beta_j Y_{t-j} + \epsilon_{YX} \ \end{align*}
자동화가능성: 여러가지 데이터에 일반화해서 자동화하기 어려움
주의사항:
무조건적 인과관계를 단정할 수 없음
시간 선후가 유의미한 맥락을 갖는 시계열에 적용할 수 있고, 시간선후 기간기준에 따라 Granger 인과관계가 있게 될 수 있음
상관관계를 두고 인과관계가 없다는 증명으로 간단히 볼 수는 있지만, 보이지 않는 요소들도 고려되어야 확실함
Granger 인과관계 테스트
가설확인
대중주장(귀무가설, Null Hypothesis, \(H_0\)): 한 변수가 다른 변수를 예측하는데 도움이 되지 않는다
나의주장(대립가설, Alternative Hypothesis, \(H_1\)): 한 변수가 다른 변수를 예측하는데 도움이 된다
의사결정(1회 검정)
p-value >= 내기준(ex. 0.05): 내가 수집한(분석한) 데이터는 대중주장과 유사하니 대중주장 참 & 나의주장 거짓
수집한(분석한) 데이터는 한 변수가 다른 변수를 예측하는데 도움되지 않는다
p-value < 내기준(ex. 0.05): 내가 수집한(분석한) 데이터는 대중주장을 벗어나니 대중주장 거짓 & 나의주장 참
수집한(분석한) 데이터는 한 변수가 다른 변수를 예측하는데 도움된다
의사결정(2회 검정 비교)
“\(Y\) lags로만 \(Y\)의 데이터를 선형회귀한 것의 예측력(p-value)” > “\(X\) lags + \(Y\) lags로 \(Y\)의 데이터를 선형회귀한 것의 예측력(p-value)”
수집한(분석한) 데이터는 \(X\)변수가 \(Y\)변수를 예측하는데 도움되지 않는다
“\(X\) lags + \(Y\) lags로 \(Y\)의 데이터를 선형회귀한 것의 예측력(p-value)” > “\(Y\) lags로만 \(Y\)의 데이터를 선형회귀한 것의 예측력(p-value)”
수집한(분석한) 데이터는 \(X\)변수가 \(Y\)변수를 예측하는데 도움된다
결과조합
“\(X\)가 \(Y\)에 인과영향을 준다” + “\(Y\)는 \(X\)에 인과영향을 주지 않는다”
: \(X\)가 \(Y\)에 선행한다고 볼 수 있기에, \(X\)가 \(Y\)의 인과요인이 될 가능성이 높음“\(Y\)가 \(X\)에 인과영향을 준다” + “\(X\)는 \(Y\)에 인과영향을 주지 않는다”
: \(Y\)가 \(X\)에 선행한다고 볼 수 있기에, \(Y\)가 \(X\)의 인과요인이 될 가능성이 높음“\(X\)가 \(Y\)에 인과영향을 준다” + “\(Y\)도 \(X\)에 인과영향을 준다”
: 쌍방으로 Granger Causality가 성립하는 경우로 이 경우 제3의 외부변수(Exogenous Variable)가 영향을 공통으로 주었을 가능성이 높음
: 제3의 외부변수(Exogenous Variable)를 알아내던가 포기하던가 해야하며, \(VAR\)모형을 사용해야 할 수 있음(Granger Causality도 \(VAR\)모형 중 하나)“\(X\)가 \(Y\)에 인과영향을 주지 않는다” + “\(Y\)도 \(X\)에 인과영향을 주지 않는다”
: 두 변수가 서로 인과영향을 주지 않는다고 볼 수도 있지만 단언은 어려움
: \(ARIMA\)모형으로 추가 확인이 가능할 수 있음
: 입력되는 최종 시차에 따라 달라질 수 있으므로 시차에 따른 해석을 달리 할 수도 있음(사람의 경험과 판단이 개입되어야 함)
실습: 닭과 달걀의 생산량을 통한 Granger 인과관계 이해¶
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
# 데이터 로딩
location = './Data/ChickenEggProduction/Chicken_Egg_Production.txt'
raw_all = pd.read_csv(location, sep='\t')
raw_all.head()
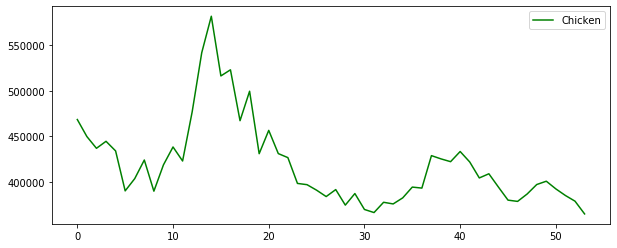
# 데이터 시각화
plt.figure(figsize=(10,4))
plt.plot(raw_all['Chicken'], 'g', label='Chicken')
plt.legend()
plt.show()
plt.figure(figsize=(10,4))
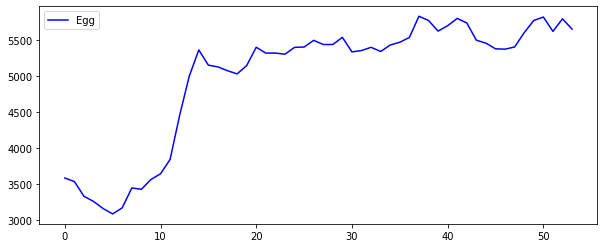
plt.plot(raw_all['Egg'], 'b', label='Egg')
plt.legend()
plt.show()
# 정상성 변환 시각화
plt.figure(figsize=(10,4))
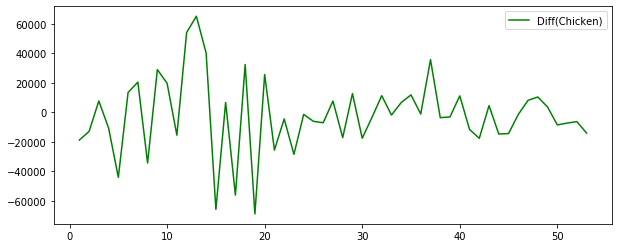
plt.plot(raw_all['Chicken'].diff(1), 'g', label='Diff(Chicken)')
plt.legend()
plt.show()
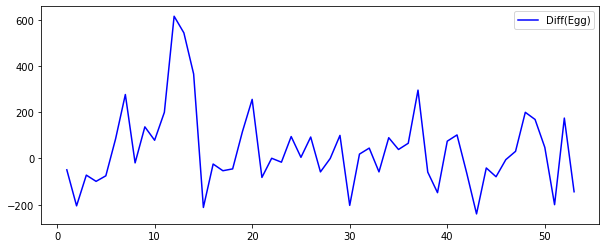
plt.figure(figsize=(10,4))
plt.plot(raw_all['Egg'].diff(1), 'b', label='Diff(Egg)')
plt.legend()
plt.show()
# Granger Causality 테스트
print('\n[Egg -> Chicken]')
granger_result1 = sm.tsa.stattools.grangercausalitytests(raw_all.diff(1).dropna().iloc[:,1:].values, maxlag=3, verbose=True)
print('\n[Chicken -> Egg]')
granger_result2 = sm.tsa.stattools.grangercausalitytests(raw_all.diff(1).dropna().iloc[:,[2,1]].values, maxlag=3, verbose=True)
# 의사결정
# 닭이 달걀을 낳으면 그 수는 약 3년후까지 닭의 수에 영향을 준다
# 닭의 수가 많아진다고해서 달걀을 많이 낳지는 않는다
# 달걀 -> 닭 (Granger Causality)
[Egg -> Chicken]
Granger Causality
number of lags (no zero) 1
ssr based F test: F=10.3694 , p=0.0023 , df_denom=49, df_num=1
ssr based chi2 test: chi2=11.0043 , p=0.0009 , df=1
likelihood ratio test: chi2=9.9819 , p=0.0016 , df=1
parameter F test: F=10.3694 , p=0.0023 , df_denom=49, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=3.9196 , p=0.0268 , df_denom=46, df_num=2
ssr based chi2 test: chi2=8.6913 , p=0.0130 , df=2
likelihood ratio test: chi2=8.0254 , p=0.0181 , df=2
parameter F test: F=3.9196 , p=0.0268 , df_denom=46, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=2.9318 , p=0.0441 , df_denom=43, df_num=3
ssr based chi2 test: chi2=10.2270 , p=0.0167 , df=3
likelihood ratio test: chi2=9.3049 , p=0.0255 , df=3
parameter F test: F=2.9318 , p=0.0441 , df_denom=43, df_num=3
[Chicken -> Egg]
Granger Causality
number of lags (no zero) 1
ssr based F test: F=0.5434 , p=0.4646 , df_denom=49, df_num=1
ssr based chi2 test: chi2=0.5766 , p=0.4476 , df=1
likelihood ratio test: chi2=0.5734 , p=0.4489 , df=1
parameter F test: F=0.5434 , p=0.4646 , df_denom=49, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=0.3865 , p=0.6816 , df_denom=46, df_num=2
ssr based chi2 test: chi2=0.8571 , p=0.6515 , df=2
likelihood ratio test: chi2=0.8500 , p=0.6538 , df=2
parameter F test: F=0.3865 , p=0.6816 , df_denom=46, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=0.2245 , p=0.8788 , df_denom=43, df_num=3
ssr based chi2 test: chi2=0.7833 , p=0.8535 , df=3
likelihood ratio test: chi2=0.7772 , p=0.8549 , df=3
parameter F test: F=0.2245 , p=0.8788 , df_denom=43, df_num=3
실습: 삼성전자와 삼성전자 우선주 Granger 인과관계 이해¶
!pip install pandas-datareader
Requirement already satisfied: pandas-datareader in c:\programdata\anaconda3\lib\site-packages (0.8.1)
Requirement already satisfied: lxml in c:\programdata\anaconda3\lib\site-packages (from pandas-datareader) (4.4.1)
Requirement already satisfied: pandas>=0.21 in c:\programdata\anaconda3\lib\site-packages (from pandas-datareader) (0.25.1)
Requirement already satisfied: requests>=2.3.0 in c:\programdata\anaconda3\lib\site-packages (from pandas-datareader) (2.22.0)
Requirement already satisfied: pytz>=2017.2 in c:\programdata\anaconda3\lib\site-packages (from pandas>=0.21->pandas-datareader) (2019.3)
Requirement already satisfied: python-dateutil>=2.6.1 in c:\programdata\anaconda3\lib\site-packages (from pandas>=0.21->pandas-datareader) (2.8.0)
Requirement already satisfied: numpy>=1.13.3 in c:\programdata\anaconda3\lib\site-packages (from pandas>=0.21->pandas-datareader) (1.16.5)
Requirement already satisfied: chardet<3.1.0,>=3.0.2 in c:\programdata\anaconda3\lib\site-packages (from requests>=2.3.0->pandas-datareader) (3.0.4)
Requirement already satisfied: certifi>=2017.4.17 in c:\programdata\anaconda3\lib\site-packages (from requests>=2.3.0->pandas-datareader) (2019.9.11)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in c:\programdata\anaconda3\lib\site-packages (from requests>=2.3.0->pandas-datareader) (1.24.2)
Requirement already satisfied: idna<2.9,>=2.5 in c:\programdata\anaconda3\lib\site-packages (from requests>=2.3.0->pandas-datareader) (2.8)
Requirement already satisfied: six>=1.5 in c:\programdata\anaconda3\lib\site-packages (from python-dateutil>=2.6.1->pandas>=0.21->pandas-datareader) (1.12.0)
WARNING: pip is being invoked by an old script wrapper. This will fail in a future version of pip.
Please see https://github.com/pypa/pip/issues/5599 for advice on fixing the underlying issue.
To avoid this problem you can invoke Python with '-m pip' instead of running pip directly.
# 데이터 로딩
import pandas_datareader.data as web
import datetime
start = datetime.datetime(2014, 1, 1)
end = datetime.datetime(2018, 12, 31)
raw1 = web.DataReader("005930.KS", 'yahoo', start, end)
raw2 = web.DataReader("005935.KS", 'yahoo', start, end)
# raw2 = web.DataReader("009150.KS", 'yahoo', start, end)
# 데이터 시각화
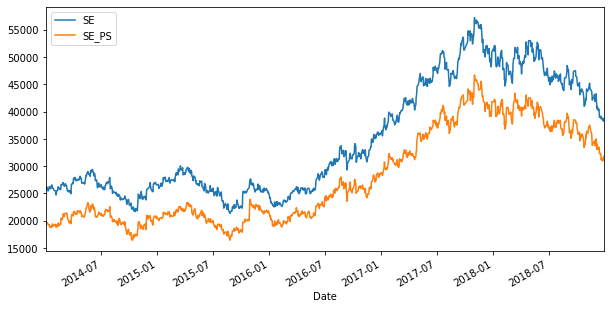
raw = pd.concat([raw1.Close, raw2.Close], axis=1).dropna()
raw.columns = ["SE", "SE_PS"]
raw.plot(figsize=(10,5))
plt.show()
# 비정상성 차수 추론
target = raw.SE.copy()
integ_result = pd.Series(sm.tsa.stattools.adfuller(target)[0:4],
index=['Test Statistics', 'p-value', 'Used Lag', 'Used Observations'])
Y1_integ_order = 0
if integ_result[1] > 0.1:
Y1_integ_order = Y1_integ_order + 1
target = raw.SE_PS.copy()
integ_result = pd.Series(sm.tsa.stattools.adfuller(target)[0:4],
index=['Test Statistics', 'p-value', 'Used Lag', 'Used Observations'])
Y2_integ_order = 0
if integ_result[1] > 0.1:
Y2_integ_order = Y2_integ_order + 1
print('Y1_order: ', Y1_integ_order, 'Y2_order: ', Y2_integ_order)
# Granger Causality 테스트
print('\n[삼성전자우 -> 삼성전자]')
granger_result1 = sm.tsa.stattools.grangercausalitytests(raw.diff(1).dropna().values, maxlag=4, verbose=True)
print('\n[삼성전자 -> 삼성전자우]')
granger_result2 = sm.tsa.stattools.grangercausalitytests(raw.diff(1).dropna().iloc[:,[1,0]].values, maxlag=4, verbose=True)
# 의사결정
Y1_order: 1 Y2_order: 1
[삼성전자우 -> 삼성전자]
Granger Causality
number of lags (no zero) 1
ssr based F test: F=3.8613 , p=0.0496 , df_denom=1216, df_num=1
ssr based chi2 test: chi2=3.8708 , p=0.0491 , df=1
likelihood ratio test: chi2=3.8647 , p=0.0493 , df=1
parameter F test: F=3.8613 , p=0.0496 , df_denom=1216, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=3.5263 , p=0.0297 , df_denom=1213, df_num=2
ssr based chi2 test: chi2=7.0818 , p=0.0290 , df=2
likelihood ratio test: chi2=7.0613 , p=0.0293 , df=2
parameter F test: F=3.5263 , p=0.0297 , df_denom=1213, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=2.6935 , p=0.0448 , df_denom=1210, df_num=3
ssr based chi2 test: chi2=8.1273 , p=0.0435 , df=3
likelihood ratio test: chi2=8.1002 , p=0.0440 , df=3
parameter F test: F=2.6935 , p=0.0448 , df_denom=1210, df_num=3
Granger Causality
number of lags (no zero) 4
ssr based F test: F=2.4757 , p=0.0427 , df_denom=1207, df_num=4
ssr based chi2 test: chi2=9.9766 , p=0.0408 , df=4
likelihood ratio test: chi2=9.9359 , p=0.0415 , df=4
parameter F test: F=2.4757 , p=0.0427 , df_denom=1207, df_num=4
[삼성전자 -> 삼성전자우]
Granger Causality
number of lags (no zero) 1
ssr based F test: F=3.7267 , p=0.0538 , df_denom=1216, df_num=1
ssr based chi2 test: chi2=3.7359 , p=0.0533 , df=1
likelihood ratio test: chi2=3.7302 , p=0.0534 , df=1
parameter F test: F=3.7267 , p=0.0538 , df_denom=1216, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=2.2516 , p=0.1057 , df_denom=1213, df_num=2
ssr based chi2 test: chi2=4.5217 , p=0.1043 , df=2
likelihood ratio test: chi2=4.5133 , p=0.1047 , df=2
parameter F test: F=2.2516 , p=0.1057 , df_denom=1213, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=1.2032 , p=0.3073 , df_denom=1210, df_num=3
ssr based chi2 test: chi2=3.6305 , p=0.3042 , df=3
likelihood ratio test: chi2=3.6251 , p=0.3049 , df=3
parameter F test: F=1.2032 , p=0.3073 , df_denom=1210, df_num=3
Granger Causality
number of lags (no zero) 4
ssr based F test: F=1.6051 , p=0.1706 , df_denom=1207, df_num=4
ssr based chi2 test: chi2=6.4681 , p=0.1668 , df=4
likelihood ratio test: chi2=6.4510 , p=0.1679 , df=4
parameter F test: F=1.6051 , p=0.1706 , df_denom=1207, df_num=4
공적분 모형(Cointegration Model)¶
공적분 상태(Cointegration): 두 비정상성 시계열을 선형조합(Linear Combination)하여 생성한 시계열의 적분(Integration) 차수가 낮아지거나 정상상태가 되는 경우
공적분 벡터(Cointegration Vector): 이러한 선형 조합을 만드는 값
공적분 시계열(Cointegration Time Series):
서로 상관관계를 가지지 않음에도 불구하고 장기적으로 같은 방향으로 움직이는 특성
술취한 사람이 개를 끈에 묶어 다니는 경우, 사람과 개는 각자 아무런 상관관계가 없이 움직이지만 서로 너무 멀어지지는 않는 것과 유사
페어 트레이딩 (Pair Trading), 통계적 차익거래 (Statistical Arbitrage) 등의 매매전략에 응용 가능
\begin{align*} \text{Each Integration Order} && Y_1 &\sim I(d_1) \ && Y_2 &\sim I(d_2) \ \text{Cointegration Vector} && \alpha &= [\alpha_1, \alpha_2] \ \text{where} && \alpha_1 x_1 &+ \alpha_2 x_2 \sim I(b), ;; b < d_1, ;; b < d_2 \ \end{align*}
공적분 판별:
Engle-Granger’s Representation Theorem (Vector Error Correction Model) \begin{align*} \text{두 시계열 \(Y_{1t} \sim I(1)\), \(Y_{2t} \sim I(1)\)이 공적분} & \iff \Delta Y_{2t} = \gamma_1 z_{t-1} + \sum_{i=1}^K \psi_{1,i} \Delta Y_{1t-i} + \sum_{i=1}^L \psi_{2,i} \Delta Y_{2t-i} + e_{t} \ & \text{(\(z_t\)는 \(Y_{2t}\)를 종속변수로 \(Y_{1t}\)를 독립변수로 회귀분석하여 만들어진 잔차)} \ \end{align*}
\(\Delta Y_{1t}\)와 \(\Delta Y_{2t}\)는 항상 정상성 시계열
위 식이 성립하려면 \(z_t\)와 \(e_t\)가 정상성 시계열이어야 함 1) \(Y_{2t}\)를 종속변수로 \(Y_{1t}\)를 독립변수로 회귀분석하여 만들어진 잔차 \(z_t\)가 정상성 시계열인지를 확인 2) 변환된 변수들의 \(VECM\) 회귀 분석의 잔차 \(e_t\)가 정상성 시계열인지를 확인
실습: Cointegration 데이터 생성 및 이해¶
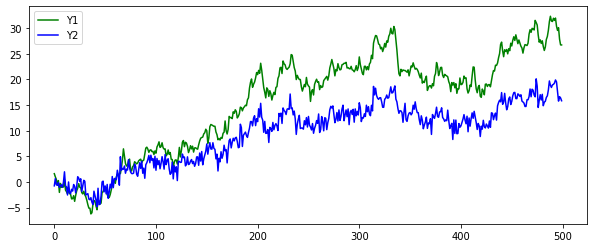
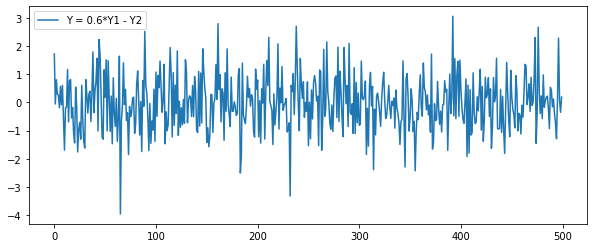
\begin{align*} \text{Example of Cointegration} \ \text{Y1: Random Walk with I(1)} && Y_{1t} &= Y_{1t-1} + e_{1t} \ \text{Y2: Random Walk with I(1)} && Y_{2t} &= 0.6 Y_{1t} + e_{2t} \ \text{Y: Stationary Time Series} && Y &= 0.6 Y_{1t} - Y_{2t} \ \end{align*}
# 데이터 생성
np.random.seed(1)
Y1 = np.random.randn(500).cumsum()
Y2 = 0.6 * Y1 + np.random.randn(500)
Y = 0.6 * Y1 - Y2
# 시각화
plt.figure(figsize=(10,4))
plt.plot(Y1, 'g', label='Y1')
plt.plot(Y2, 'b', label='Y2')
plt.legend()
plt.show()
plt.figure(figsize=(10,4))
plt.plot(Y, label='Y = 0.6*Y1 - Y2')
plt.legend()
plt.show()
# VECM 공적분 확인
coint_result = sm.tsa.coint(Y1, Y2)
pd.DataFrame([coint_result[0], coint_result[1]], index=['statistics', 'p-value'], columns=['output'])
| output | |
|---|---|
| statistics | -22.680907 |
| p-value | 0.000000 |
실습: 페어 트레이딩 Cointegration 모형화 및 해석¶
# 데이터 로딩
import pandas_datareader.data as web
import datetime
start = datetime.datetime(2014, 1, 1)
end = datetime.datetime(2018, 12, 31)
raw1 = web.DataReader("005930.KS", 'yahoo', start, end)
raw2 = web.DataReader("005935.KS", 'yahoo', start, end)
# raw2 = web.DataReader("009150.KS", 'yahoo', start, end)
# 데이터 시각화
## 시계열 움직임
raw = pd.concat([raw1.Close, raw2.Close], axis=1).dropna()
raw.columns = ["SE", "SE_PS"]
raw.plot(figsize=(10,5))
plt.show()
## 비교 움직임
plt.figure(figsize=(8,6))
plt.plot(raw.SE, raw.SE_PS, alpha=0.7)
plt.scatter(raw.SE.values[-1:], raw.SE_PS.values[-1:], c="r", s=300)
plt.show()
# 비정상성 차수 추론
target = raw.SE.copy()
integ_result = pd.Series(sm.tsa.stattools.adfuller(target)[0:4],
index=['Test Statistics', 'p-value', 'Used Lag', 'Used Observations'])
Y1_integ_order = 0
if integ_result[1] > 0.1:
Y1_integ_order = Y1_integ_order + 1
target = raw.SE_PS.copy()
integ_result = pd.Series(sm.tsa.stattools.adfuller(target)[0:4],
index=['Test Statistics', 'p-value', 'Used Lag', 'Used Observations'])
Y2_integ_order = 0
if integ_result[1] > 0.1:
Y2_integ_order = Y2_integ_order + 1
print('Y1_order: ', Y1_integ_order, 'Y2_order: ', Y2_integ_order)
# 회귀분석 적합
## 모델링
Y = raw.SE
X = raw.SE_PS
X = sm.add_constant(X)
fit = sm.OLS(Y, X).fit()
display(fit.summary())
## 회귀분석 시각화
import seaborn as sns
plt.figure(figsize=(10,7))
sns.regplot(x="SE_PS", y="SE", data=raw)
plt.tight_layout()
plt.show()
# 공적분 시계열 시각화
Y_integ = raw.SE - fit.params[1]*raw.SE_PS
plt.figure(figsize=(10,7))
Y_integ.plot()
plt.show()
# 공적분 시계열 비정상성 테스트
target = fit.resid
display(pd.Series(sm.tsa.stattools.adfuller(target)[0:4],
index=['Test Statistics', 'p-value', 'Used Lag', 'Used Observations']))
# VECM 공적분 테스트
coint_result = sm.tsa.coint(raw.SE, raw.SE_PS)
pd.DataFrame([coint_result[0], coint_result[1]], index=['statistics', 'p-value'], columns=['output'])
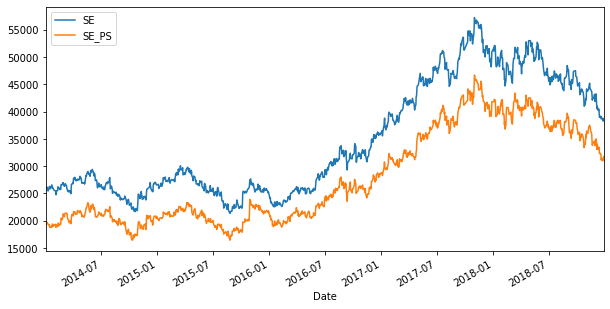

Y1_order: 1 Y2_order: 1
| Dep. Variable: | SE | R-squared: | 0.991 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.991 |
| Method: | Least Squares | F-statistic: | 1.295e+05 |
| Date: | Fri, 13 Mar 2020 | Prob (F-statistic): | 0.00 |
| Time: | 23:33:27 | Log-Likelihood: | -10165. |
| No. Observations: | 1221 | AIC: | 2.033e+04 |
| Df Residuals: | 1219 | BIC: | 2.034e+04 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 915.1881 | 97.943 | 9.344 | 0.000 | 723.033 | 1107.344 |
| SE_PS | 1.2147 | 0.003 | 359.877 | 0.000 | 1.208 | 1.221 |
| Omnibus: | 11.477 | Durbin-Watson: | 0.124 |
|---|---|---|---|
| Prob(Omnibus): | 0.003 | Jarque-Bera (JB): | 10.735 |
| Skew: | -0.189 | Prob(JB): | 0.00467 |
| Kurtosis: | 2.738 | Cond. No. | 9.94e+04 |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 9.94e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
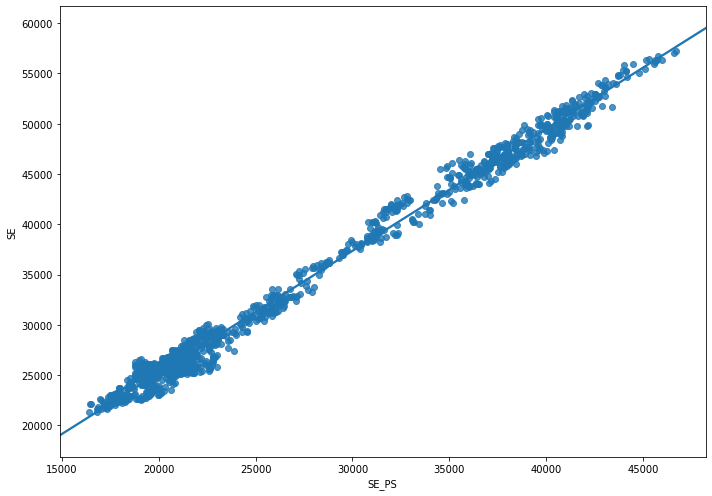
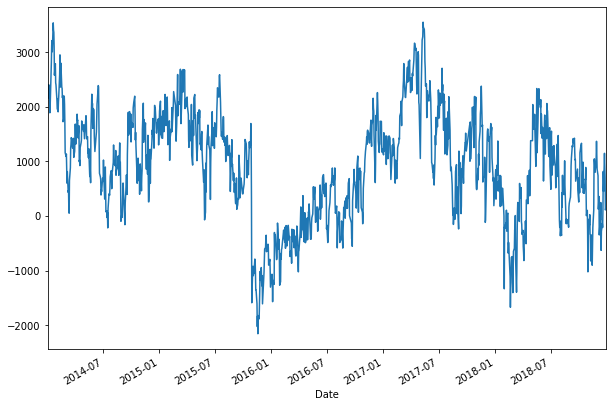
Test Statistics -3.742838
p-value 0.003549
Used Lag 9.000000
Used Observations 1211.000000
dtype: float64
| output | |
|---|---|
| statistics | -3.743068 |
| p-value | 0.016116 |